В этом уроке мы познакомимся с задачами на движение в противоположных направлениях.

При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».

Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.

Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.

Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.

В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.

При решении задач на движение в противоположных направлениях, используют еще одно понятие «скорость удаления».

Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени. Обозначается ʋуд..

Чтобы найти скорость удаления, зная скорости объектов, надо найти сумму этих скоростей: ʋуд. = ʋ1 + ʋ2. Чтобы найти скорость удаления, зная время и расстояние, необходимо расстояние разделить на время: ʋуд. = S : t.

Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на движение в противоположных направлениях.

ЗАДАЧА 1. Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и то же время грузовик проехал 70 км, а легковой автомобиль – 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика – 35 км/ч?

Изобразим движение грузового и легкового автомобиля на схеме.

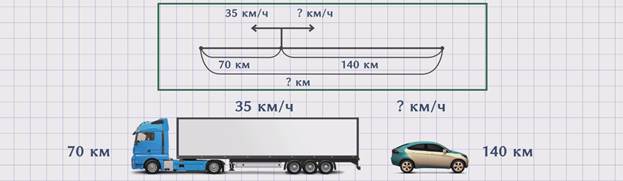
Скорость грузового автомобиля обозначим буквой ʋ1 = 35 км/ч. Скорость легкового автомобиля обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t. Расстояние, которое проехал грузовой автомобиль - буквой S1 = 70 км. Расстояние, которое проехал легковой автомобиль – S2 = 140 км.

Разберем первый вариант.

Поскольку, чтобы найти неизвестную скорость, необходимо знать расстояние, которое проехал легковой автомобиль, а оно известно и равно 140 км, и знать время движения, которое не указано в условиях задачи, то необходимо найти это время.Из условия задачи нам известно расстояние, которое проехал грузовой автомобиль S1 = 70 км и скорость грузового автомобиля ʋ1 = 35 км/ч. Используя эти данные, мы можем найти время. t = S1 : ʋ1 = 70 : 35 = 2 часа. Зная время и расстояние, которое проехал легковой автомобиль, мы сможем узнать скорость легкового автомобиля, так как ʋ2 = S2 : t = 140 : 2 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.

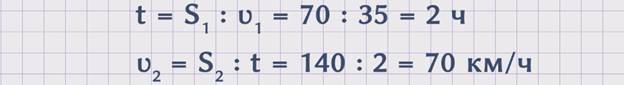
Рассмотрим второй вариант.

Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость грузового автомобиля, из условий задачи она известна, и скорость удаления, которая не оговаривается условиями задачи, то надо найти скорость удаления. Чтобы найти скорость удаления автомобилей, можно расстояние, которое проехали оба автомобиля, разделить на время. ʋуд. = S : t . Расстояние, которое проехали оба автомобиля, равно сумме расстояний S1 и S2. S = S1 + S2 = 70 + 140 = 210 км. Время можно узнать, разделив расстояние, которое проехал грузовой автомобиль, на его скорость. t = S1 : ʋ1 = 70 : 35 = 2 часа. Значит, ʋуд. = S : t = 210 : 2 = 105 км/ч. Теперь, зная скорость удаления, можем найти скорость легкового автомобиля. ʋ2 = ʋсбл. - ʋ1 = 105 – 35 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.

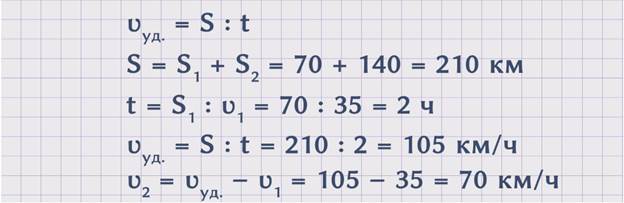
ЗАДАЧА 2. Два человека в одно и то же время вышли из поселка в разных направлениях. Один двигался со скоростью 6 км/ч, скорость другого была 5 км/ч. Сколько часов понадобится, чтобы расстояние между ними стало 33 км?

Изобразим движение людей на схеме.

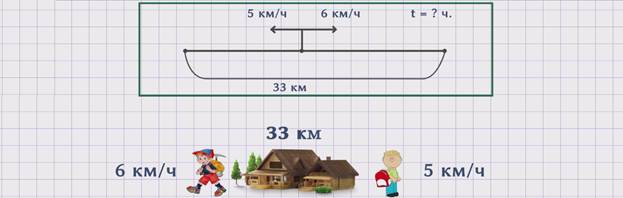
Скорость первого человека обозначим буквой ʋ1 = 5 км/ч. Скорость второго человека обозначим буквой ʋ2 = 6 км/ч. Расстояние, которое они прошли, обозначим буквой S = 33 км. Время – буквой t = ? часов.

Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость удаления, так как t = S : ʋуд.. Поскольку расстояние нам известно из условия задачи, надо найти скорость удаления. ʋуд. = ʋ1 + ʋ2 = 5 + 6 = 11 км/ч. Теперь зная скорость удаления, можем найти неизвестное время. t = S : ʋуд = 33 : 11 = 3 ч. Получаем, что понадобилось 3 часа, чтобы расстояние между людьми стало 33 км.

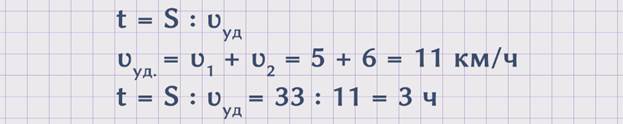
ЗАДАЧА 3. Два поезда одновременно начали движение в противоположных направления с разных станций, расстояние между которыми составляет 25 км. Один двигался со скоростью 160 км/ч. На каком расстоянии друг от друга поезда будут через 4 часа, если скорость другого поезда – 130 км/ч?

Покажем движение поездов на схеме.

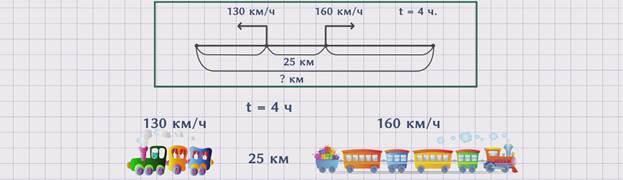
Скорость первого поезда обозначим буквой ʋ1 = 130 км /ч. Скорость второго поезда обозначим ʋ2 = 160 км/ч. Расстояние между станциями обозначим буквой Sм = 25 км. Время – буквой t = 4 часа. А искомое расстояние – буквой S = ? км.

Чтобы ответить на вопрос задачи, необходимо знать расстояние между станциями, расстояние, которое проехал первый поезд, и расстояние, которое проехал второй поезд, так как S = Sм + S1 + S2. Расстояние между станциями известно из условия задачи, а расстояния S1 и S2 нет, но их можно найти, используя другие данные задачи. Однако искомое расстояние можно найти более рациональным путем, а именно сложив расстояние между станциями и общее расстояние, которое проехали оба поезда, так как S = Sм + Sоб.. Поскольку расстояние между станциями известно из условия задачи, надо найти общее расстояние. Для этого необходимо время умножить на скорость удаления. Sоб = t · ʋуд. А скорость удаления равна сумме скоростей поездов. ʋуд. = ʋ1 + ʋ2 = 160 + 130 = 290 км/ч. Теперь можем найти общее расстояние Sоб = t · ʋуд.= 4 · 290 = 1160 км.Зная общее расстояние, можем найти искомое расстояние. S = Sм + Sоб = 25 + 1160 = 1185 км. Получили, что через 4 часа расстояние между поездами будет составлять 1185 км.

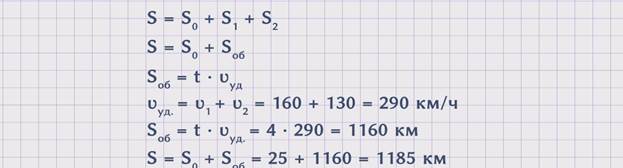
При решении задач на движение в противоположных направлениях, следует помнить, что в задачах такого типа выполняются следующие условия:

1)объекты начинают свое движение одновременно в противоположных направлениях, а значит, находятся в пути одинаковое количество времени; время обозначается латинской буквой t = S : ʋуд;

2)расстояние S – это сумма всех расстояний, оговоренных условиями задачи; 

S = S1 + S2 + Sмили S = ʋуд. · t;

3)объекты удаляются с определенной скоростью – скоростью удаления, обозначающейся латинской буквой ʋуд. = S : t или ʋуд = ʋ1 + ʋ2, соответственно

ʋ1 = S1 : t и ʋ2 = S2 : t.