Изучим на этом уроке, какая пирамида называется усеченной и как ее получить из обычной пирамиды. Посмотрим, из каких частей состоит усеченная пирамида, а так же дадим определение правильной усеченной пирамиды.

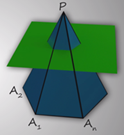
Итак, в словосочетании усеченная пирамида, само слово усеченная предполагает, что пирамиду взяли и каким-то образом усекли. Действительно, чтобы получить усеченную пирамиду достаточно провести сечение пирамиды параллельно плоскости основания. Посмотрите что получится, если мы в пирамиде PА1А2…Аn проведем сечение параллельное плоскости основания А1А2…Аn, пересекающее боковые ребра в точках В1, В2, …, Bn. Видим на рисунке два выпуклых многогранника :

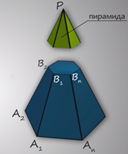
Один, из которых является пирамидой подобной нашей начальной пирамиде, а вот второй многогранник как раз и будет называться усеченной пирамидой. Рассмотрим более подробно, из каких частей состоит данная фигура (рис. 3).

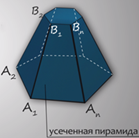
Этими составными частями будут два n-угольника А1А2…Аn и В1В2…Вn, назовем их основаниями усеченной пирамиды и n четырехугольников их мы назовем боковыми гранями. Мы готовы дать определение усеченной пирамиды. Многогранник, гранями которого являются n-угольники А1А2…Аn и В1В2…Вn (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n четырехугольников А1А2В2В1, А2А3В3В2,…, АnА1В1Вn (боковые грани), называется усеченной пирамидой.

После того как мы дали понятие усеченной пирамиды попробуем найти и в нашей жизни что-то похожее на усеченную пирамиду. Рассмотрим лишь некоторые предметы, имеющие форму усеченной пирамиды. Примером усеченной пирамиды может служить уличный фонарь или вытяжка над варочной поверхностью кухонной плиты, так же можно сказать, что кнопка клавиатуры тоже представляет собой усеченную пирамиду. И даже вкусный кекс к празднику может иметь форму усеченной пирамиды.

Для решения задач и доказательства утверждений не достаточно тех элементов усеченной пирамиды, о которых мы сказали ранее, поэтому пополним свою копилку знаний и дадим еще несколько определений касающихся усеченной пирамиды. Отрезки А1В1, А2В2, …, называются боковыми ребрами усеченной пирамиды. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды. На рисунке СН является высотой усеченной пирамиды А1А2…АnВ1В2…Вn.

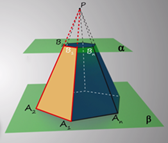
Каждая из боковых граней усеченной пирамиды будет являться трапецией и это можно доказать. Рассмотрим боковую грань А1А2В2В1. Стороны А1А2 и В1В2 параллельны, поскольку принадлежат прямым, по которым плоскость РА1А2 пересекается с параллельными плоскостями α [альфа] и β [бета]. Две другие стороны А1В1 и А2В2 этой грани не параллельны – их продолжения пересекаются в точке Р .

Четырехугольник, у которой две стороны параллельны, а две другие нет, называется трапецией, из чего следует, что боковые грани усеченной пирамиды являются трапециями.

Когда мы рассматривали пирамиду, то выделяли из множества пирамид правильную пирамиду. Среди усеченных пирамид тоже можно выделить правильные усеченные пирамиды. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами. Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней. Мы знаем, что в математике, а тем более в геометрии любое утверждение требует доказательства, если оно не является аксиомой. Именно доказательством данных утверждений мы и займемся на следующем уроке.

Хочется отметить, что ни одна геометрическая фигура не изучается ради самой фигуры. Все в математике изучается для практической необходимости. И было приведено немало примеров, где в жизни можно встретить усеченную пирамиду. К слову сказать, параметры уличного фонаря необходимо знать, чтобы правильно подобрать лампочку, которую будут использовать для освещения. Когда выпекают вкусный кекс в большой или малой форме, нужно знать, сколько приготовить продуктов для бисквита. И вообще, исходя из размеров кекса, хватит ли его нашим гостям.

Итоги:

Усеченная пирамида – это многогранник, гранями которого являются n-угольники А1А2…Аn и В1В2…Вn (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n четырехугольников А1А2В2В1, А2А3В3В2,…, АnА1В1Вn (боковые грани).

Боковая грань усеченной пирамиды является трапецией, т.к. четырехугольник, у которого две стороны параллельны, а две другие нет, называется трапецией.

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами