Стоит, столетья за собой сжигая.

Стоит не первый и не третий век.

Взглянув, одно дыханье замирает.

Какое чудо создал человек.

Стихотворение это было найдено на просторах интернета. Удивительно, как точно автор описывает пирамиду. Поставим и перед собой задачу на этом уроке изучить, что такое пирамиды, рассмотреть её элементы, вывести формулу для вычисления площади полной поверхности пирамиды.

Думаю, у большинства из нас первой игрушкой в жизни была пирамидка. На уроках истории происходило знакомство со знаменитыми египетскими пирамидами, одним из чудес света. 

Образ пирамиды используются в архитектуре и в наше время – башни Кремля, церковь преображения в Кижах, пирамида Лувра, храм Махабодхи, санаторий в Санкт Петербурге, станция метро в Мюнхене. Форму пирамиды используют и при огранке драгоценных камней.

Есть одна восточная пословица, которая гласит «Всё на свете боится времени, но время боится египетских пирамид». Действительно египетские пирамиды были построены в 26в. до н.э., но до сих пор мы восхищаемся их величием, красотой и монументальностью. Древние греки считали пирамиды первым из семи чудес света. Архитектурные памятники последующих эпох, в том числе крупнейший христианский храм Европы — собор Святого Петра в Риме, кажутся карликами рядом с пирамидой Хеопса, основание которой в два раза превосходит по ширине Красную площадь в Москве.

Все сведения, факты, цифры и домыслы отступают на второй план при непосредственной встрече с пирамидами. Один из спутников Наполеона в его египетском походе с 1798—1799 гг., французский учёный Франсуа Жомар, записал: «...когда вы подойдёте к подошве великой пирамиды, вас охватывает глубокое и сильное волнение, чувство потрясения и подавленности, вызываемые величием и простотой форм, контрастом между человеком и колоссальным творением рук его; глаз не может его охватить, мысль с трудом может объять его...».

Существует большое количество действительно огромных пирамид, как современных, так и древних. Определить самые большие из них можно по множеству параметров, самым простым из которых будет просто замерять высоту.

Пирамида – это один из важных видов многогранника. Сложный и простой одновременно.

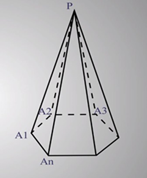
Рассмотрим многоугольник А1А2А3…Аn и точку Р, не лежащую в плоскости этого многоугольника, получим n треугольников РА1А2, РА2А3,…РАn-1An, РАnA1. Многогранник составленный из n-угольника А1А2А3…Аn и n треугольников называется пирамидой. Многоугольник А1А2А3…Аn называется основанием пирамиды, треугольники РА1А2, РА2А3,… РАnA1 боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА1, РА2, …РАn – её боковыми ребрами.

Пирамиду с основанием А1А2А3…Аn и вершиной Р обозначают так: РА1А2А3…Аn и называют n-угольной пирамидой.

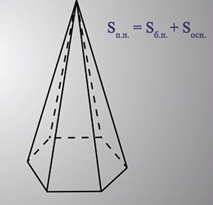
Встретилось еще одно математическое понятие, как высота пирамиды. Итак, высота пирамиды – это перпендикуляр, проведенный из вершины пирамиды к плоскости основания.

Введем еще одно понятие как площадь полной поверхности пирамиды. Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (то есть основания и боковых граней), а площадью боковой поверхности – сумма площадей ее боковых граней.

Значит можно сказать, что площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания.

Классифицировать пирамиды можно несколькими способами. Например, в зависимости от того, какой многоугольник лежит в основании, пирамиды могут быть треугольными, четырехугольными, и вообще, n-угольными.

А еще, бывают пирамиды правильные, о них у нас будет отдельный урок. Существует и еще один интересный вид пирамид – это пирамиды усеченные. Спросите что это такое?

Это когда взяли произвольную пирамиду и провели сечение параллельно основанию. Нижний получившийся многогранник и будет считаться усеченной пирамидой.

Это когда взяли произвольную пирамиду и провели сечение параллельно основанию. Нижний получившийся многогранник и будет считаться усеченной пирамидой.

Примером может послужить целое архитектурное строение Кафедральный собор Сан Себастьяна в Рио-де-Жанейро или же кнопка от компьютерной клавиатуры. Закончить урок хотелось бы еще одним популярным в интернете стихотворением :

«Я видел картину.

На этой картине

Стоит пирамида в песчаной пустыне.

Всё в пирамиде необычайно,

Какая-то есть в ней загадка и тайна.

А Спасская башня на площади Красной,

И детям, и взрослым знакома прекрасно.

Посмотришь на башню, обычная с виду,

А что на вершине у ней? Пирамида!»