На этом уроке рассмотрим правильные многогранники , а именно симметрию таких фигур. Поговорим о том, кто в своем творчестве обращался к гармонии и красоте правильных многогранников.
Напомним определение правильного многогранника и вспомним, какие именно правильные многогранники существуют и изучаются в геометрии.
Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер. Правильных многогранников всего пять: тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр.
Напомним так же, о каких видах симметрии мы говорим в пространстве – это симметрия центральная (относительно точки), осевая симметрия (относительно прямой) и симметрия относительно плоскости.
Рассмотрим элементы симметрии правильного тетраэдра. Он не имеет центра симметрии. Зато прямая, проходящая через середины двух противоположных ребер, является его осью симметрии.
Плоскость![]() , проходящая через ребро АВ перпендикулярно к противолежащему ребру СD правильного тетраэдра АВСD, является плоскостью симметрии. Посмотрите, правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.
, проходящая через ребро АВ перпендикулярно к противолежащему ребру СD правильного тетраэдра АВСD, является плоскостью симметрии. Посмотрите, правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.
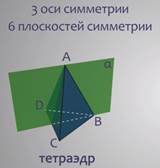
Куб имеет один центр симметрии – точку пересечения его диагоналей. Прямые а и b, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Обратите внимание, все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии. Оставшиеся три правильных многогранника так же имеют центр симметрии и несколько осей и плоскостей симметрии. Попробуйте посчитать их число.
Изучение многогранников увлекало многих творческих людей. Знаменитый художник Альбрехт Дюрер в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр. Перед вами изображение картины художника Сальвадора Дали "Тайная Вечеря". Это огромное полотно, в котором художник решил посоревноваться с Леонардо да Винчи. Обратите внимание, что изображено на переднем плане картины. Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. Голландский художник Мориц Корнилис Эшер, родившийся в 1989 году в Леувардене, создал уникальные и очаровательные работы, в которых использован или показан широкий круг математических идей. Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные. В начале XX века во Франции зародилось модернистское направление в изобразительном искусстве, прежде всего в живописи – кубизм, характеризующийся использованием подчеркнуто геометризованных условных форм, стремлением «раздробить» реальные объекты на стереометрические примитивы. Наиболее известными кубистическими произведениями стали картины Пикассо «Авиньонские девицы», «Гитара».
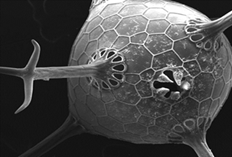
Природа создает не менее восхищающие творения. Поваренная соль состоит из кристаллов в форме куба. Скелет одноклеточного организма феодарии представляет собой икосаэдр. Минерал сильвин также имеет кристаллическую решетку в форме куба. Кристаллы пирита имеют форму додекаэдра. Молекулы воды имеют форму тетраэдра.
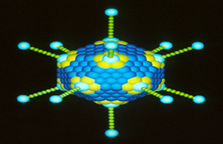
Минерал сильвин также имеет кристаллическую решетку в форме куба. Кристаллы пирита имеют форму додекаэдра. Молекулы воды имеют форму тетраэдра. Минерал куприт образует кристаллы в форме октаэдров. Вирусы, построенные только из нуклеиновой кислоты и белка, имеют вид икосаэдра.Всем этим мы можем любоваться и восхищаться повсюду.
И в который раз хочется вернуться к словам Иоганна Кеплера немецкого математика, астронома, механика, оптика и астролога, первооткрывателя законов движения планет, который сказал «Математика есть прообраз красоты мира.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!