На уроке мы познакомимся с понятием площадь поверхности призмы, площадь боковой поверхности призмы, а так же выведем формулы для их отыскания.

Нахождение площади какой-либо поверхности практическая необходимость в различных сферах жизни. Для того чтобы оклеить комнату обоями нам необходимо знать площадь боковой поверхности этой комнаты, т.е. площадь стен.

Чтобы покрасить бак, поверхность которого представляет собой призму, нужно знать площадь полной поверхности этого бака, и только тогда, зная расход краски, мы узнаем сколько нам ее понадобится.

Вообще, площадь поверхности призмы складывается из площадей всех граней призмы.

У n-угольной призмы два основания и n параллелограммов образующих боковую поверхность. Значит, площадь полной поверхности n-угольной призмы складывается из площадей двух оснований и n параллелограммов расположенных в боковых гранях.

Сумма площадей боковых граней называется площадью боковой поверхности. Тогда нахождение площади полной поверхности призмы можно выразить формулой:

площадь полной поверхности равна сумме двух площадей оснований и площади боковой поверхности.

Sполн. =2Sосн. +Sбок.

Более подробно рассмотрим прямую призму. Вычислить площадь боковой поверхности прямой призмы, складывая площади прямоугольников каждый раз было бы очень длительно и требовало бы большой траты времени, поэтому в математике была выведена формула для отыскания площади боковой поверхности прямой призмы.

Итак, докажем теорему о площади боковой поверхности прямой призмы. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту. 

Sбок =P∙h

Для того чтобы иллюстрировать теорему рассмотрим прямую треугольную призму, а точнее её развертку.

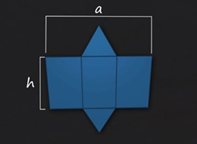
Из рисунка видно, что площадь боковой поверхности равна площади прямоугольника, одной стороной которого является боковое ребро, другой сумма ребер основания.

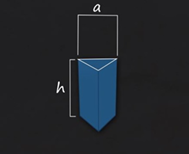
В случае прямой призмы боковое ребро является высотой. Значит, площадь боковой поверхности призмы равна произведению периметра основания на высоту.

Дадим теперь строго математическое доказательство. Боковые грани прямой призмы – прямоугольники, основания которых - стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т.е. периметр P.

Sбок=а∙h+ а∙h+ а∙h=(а+а+а)∙h=P∙h

Итак, площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. Что и требовалось доказать.

Sбок= P∙h