Еще в глубокой древности возникла необходимость вычислять стороны прямоугольных треугольников по двум известным сторонам. Такие задачи решают при проектировании и установке различных объектов. Например: нужно установить елку высотой 8 м в вертикальном положении. Для этого от вершины елки протягивают три проволочные натяжки одинаковой длины и закрепляют их на земле на расстоянии 6 м от основания елки. Нужно вычислить, какой длины должны быть проволочные натяжки.

Эту задачу мы сумеем решить, применив знаменитую теорему Пифагора. Пифагор Самосский (570—490 гг. до н. э.) — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.

Теорема Пифагоразвучит так: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Существует более ста различных способов доказательства этой теоремы. Рассмотрим один из них.

Дан прямоугольный треугольник с катетами а, в и гипотенузой с. 

Докажем, что с2 = а2 + в2. 

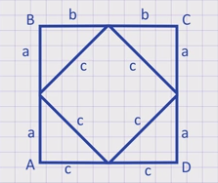
Для доказательства достроим треугольник до квадрата АВСД со стороной а + в так, как показано на рисунке. Площадь этого квадрата равна (а + в)2 . Он состоит из четырех равных прямоугольных треугольников и квадрата со стороной с. 

Площадь каждого прямоугольного треугольника равна ½ ав, а площадь квадрата со стороной с равна с2.

По свойству площадей: если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников, получим, что площадь того же квадрата АВСД равна 4 ·½ ав + с2 = 2ав + с2. Таким образом, (а + в)2 = 2ав+ с2, откуда с2 = а2 + в2. Теорема доказана.

Из истории: Сохранилось предание, заключенное в стихотворных строках, автор которых неизвестен: «В день, когда Пифагор открыл свой чертёж знаменитый, Славную он за него жертву быками воздвиг». Однако, несмотря на то, что эта теорема связывается с именем Пифагора, она уже встречалась в вавилонских текстах за 1200 лет до великого математика. Быть может, тогда не знали о доказательствах, и это соотношение получили опытным путем, а Пифагору удалость его доказать.

Теорема Пифагора позволяет по двум сторонам прямоугольного треугольника находить третью. 

Иногда в геометрии встречаются задачи, где нужно определить по длинам сторон треугольника, будет ли он прямоугольным.

Например, будет ли треугольник со сторонами 6, 8, 10 прямоугольным? При решении таких задач применяется теорема, обратная теореме Пифагора: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Проверим справедливость равенства: 102 = 82 + 62, равенство справедливое 100 = 64 + 36, значит, треугольник со сторонами 6, 8, 10 является прямоугольным.

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, получили называние пифагоровы треугольники. Например: 5, 12, 13 или 8, 15, 17 и т.д.

Прямоугольный треугольник с соотношением сторон 3:4:5 называют египетским треугольником, так как он был известен еще древним египтянам.

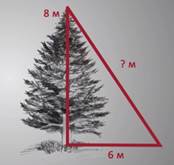
А теперь вернемся к задаче о елке, которая прозвучала в начале нашего урока. Так как елку устанавливают перпендикулярно к земле, то будем рассматривать прямоугольный треугольник АВС, где катет АС – расстояние от основания елки до натянутой проволоки, закрепленной в земле, катет ВС – высота елки, гипотенуза АВ – длина проволочной натяжки, которую надо вычислить.