В этом уроке познакомимся с теоремой о площади треугольника, запишем формулы и рассмотрим решение задачи на вычисление площади треугольника.

Начертим треугольник АВС, из точки С проведем перпендикуляр СH к стороне АВ.

Сторону АВ будем называть основанием, а перпендикуляр СН – высотой треугольника.

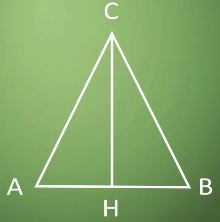
Рассмотрим теорему о площади треугольника:

Площадь треугольника равна половине произведения его основания на высоту.

Докажем это утверждение.

Дан треугольник АВС, АВ – основание, СН – высота.

Нужно доказать:

Доказательство:

Достроим треугольник АВС до параллелограмма АВDС.

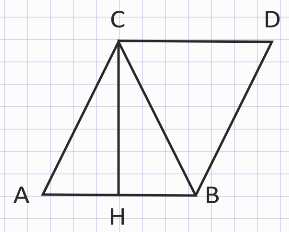
Треугольники АВС и DСВ равны по третьему признаку равенства треугольников (у них сторона ВС является общей, АВ = СD и АС = ВD как противоположные стороны параллелограмма), поэтому площади треугольников АВС и DСВ равны.

Следовательно, площадь треугольника АВС равна половине площади параллелограмма АВDС, а площадь параллелограмма равна произведению его основания на высоту, значит, площадь S треугольника АВС равна 1/2 АВ*СН. Что и требовалось доказать.

У рассмотренной теоремы о площади треугольника есть два следствия.

Одно касается площади прямоугольного треугольника, а второе – отношения площадей треугольников.

Следствие 1:

Площадь прямоугольного треугольника равна половине произведения его катетов.

Таким образом, для вычисления площади прямоугольного треугольника применяют следующую формулу:

Следствие 2:

Если высоты двух треугольников равны, то их площади относятся как основания.

В геометрии есть еще одно утверждение относительно отношения площадей треугольников – это следующая теорема:

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Решим задачу:

В треугольнике АВС угол С равен 45°, высота АD делит сторону СВ на отрезки СD = 8 см, DВ = 6 см.

Найдите площадь треугольника.

Для вычисления площади треугольника АВС необходимо знать длину высоты АD. Рассмотрим прямоугольный треугольник АСD.

Он равнобедренный, поскольку его углы САD и DСА при основании АС равны. Действительно, угол САD как и угол DСА, он же угол С, тоже равен 45°=180° – (угол АDС + угол С)=180° – (90°+45°).

Так как треугольник АСD равнобедренный, то АD = СD = 8 см.

Площадь S треугольника АВС равна ½ ВС*АD, а ВС = СD + DВ = 8 + 6 = 14 см.

Подставив найденные величины в формулу, получим: площадь треугольника равна 14*8/2=56 см2.

Иногда в геометрии встречаются задачи на вычисление площади треугольника, где даны все три его стороны.

При решении таких задач используют формулу Герона.

Герон Александрийский (I-II вв. н. э.) – древнегреческий инженер, физик, механик, математик, изобретатель.

При вычислении площади равностороннего треугольника используют формулу:

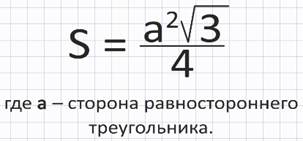
Итак, на этом уроке Вы познакомились с теоремой о площади треугольника и её следствиями, с утверждениями об отношении площадей треугольников, записали формулы нахождения площади треугольников и решили соответствующую задачу.