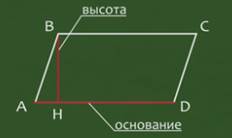
Начертим параллелограмм АВСD, из точки В проведем перпендикуляр ВH к стороне АD.

Сторону АD будем называть основанием, а перпендикуляр ВН – высотой параллелограмма.

Рассмотрим теорему для вычисления площади параллелограмма.

Теорема: Площадь параллелограмма равна произведению его основания на высоту.

Докажем это утверждение. 

Дано: параллелограмм АВСD, АD – основание, ВН – высота.

Доказать:S = АD·ВН.

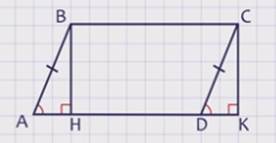
Доказательство:

В данном параллелограмме проведем еще одну высоту СК к стороне АD. Получилась трапеция АВСК, состоящая из параллелограмма АВСD и треугольника DСК. С другой стороны эта трапеция составлена из прямоугольника ВСКН и треугольника АВН. Треугольники АВН и DСК – прямоугольные и равны по гипотенузе и острому углу, действительно, гипотенузы АВ и СD равны как противоположные стороны параллелограмма, а углы ВАН и СDК равны как соответственные углы при пересечении параллельных прямых АВ и СD секущей АD. Значит, площади этих прямоугольных треугольников равны. Следовательно, площадь параллелограмма АВСD равна площади прямоугольника ВСКН. По теореме о площади прямоугольника S = ВС · ВН, а так как ВС = АD, то S = АD · ВН, т.е. площадь параллелограмма равна произведению основания на высоту. 

Что и требовалось доказать.

Решим задачу.

Задача: Смежные стороны АD и АВ параллелограмма АВСD равны соответственно 32см и 26 см, а один из углов равен 150°. Найдите площадь параллелограмма.

Решение:

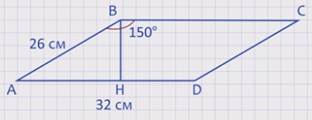
Для решения данной задачи из известного нам тупого угла, пусть это будет угол В, проведем высоту ВН и рассмотрим получившийся прямоугольный треугольник АВН. Угол АВН = 150° – 90° = 60°, тогда угол ВАН = 180° – (90° + 60°) = 30°. По свойству прямоугольного треугольника ВН равна половине гипотенузы АВ, т.е. ВН = 26/2 = 13 см. А площадь параллелограмма равна произведению основания АD на высоту ВН, S= 32 · 13 = 416 см2. 

Ответ: площадь параллелограмма равна 416 см2.