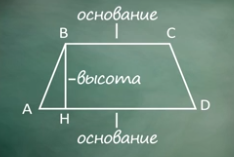
Начертим трапецию АВСD, АD и ВС - основания трапеции, проведем перпендикуляр ВН к основанию АD.

Перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание, называют высотой трапеции.

ВН – это высота трапеции.

Рассмотрим теорему о площади трапеции.

Теорема:Площадь трапеции равна произведению полусуммы её оснований на высоту.

Докажем это утверждение. 

Дано: трапеция АВСD, АD и ВС – основания, ВН – высота.

Доказать: площадь трапеции АВСD будет равна S = ½ (АD + ВС) · ВН.

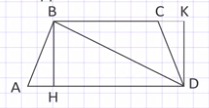
Доказательство: проведем диагональ ВD, она делит трапецию на два треугольника АВD и ВСD. Значит, площадь трапеции АВСD будет равна сумме площадей этих треугольников.

В треугольнике АВD: АD является основанием, а ВH - высотой; в треугольнике ВСD: ВС – основание, проведем высоту DК. Площадь S треугольника АВD = 1/2 АD · ВН; площадь S треугольника ВСD = 1/2 ВС · DК. Так как ВН = DК, то площадь S треугольника ВСD = 1/2 ВС · ВН. Таким образом, площадь S трапеции АВСD = 1/2 АD · ВН + 1/2 ВС · ВН = 1/2 (АD + ВС) · ВН. 

Что и требовалось доказать.

Решим задачу.

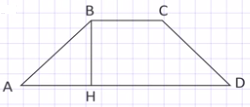
Задача:в равнобедренной трапеции АВСD∠В равен 135°, а высота ВH делит основание АD на отрезки АН = 3 см и НD= 9 см. Найдите площадь трапеции.

Решение: Так как ВН высота трапеции, то ∠В, равный 135°, делится на ∠АВН = 45° и ∠НВС = 90°. ∠А = 45°=∠АВН (т.к. в прямоугольном треугольнике АВН ∠А = 180° – (90° + 45°) = 45°). Следовательно, треугольник АВН равнобедренный и АН = ВН = 3 см. Проведем еще одну высоту нашей трапеции СК, которая разделит отрезок НDна два отрезка НК и КD, НК= НD – КD.

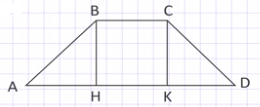
Отрезки АН и КD равные, т.к. по условию трапеция равнобедренная, и равны 3 см. Тогда отрезок НК = 9 – 3 = 6см. Отрезки НК и ВС равны, как противоположные стороны прямоугольника. Таким образом, получаем нижнее основание АD = АН + НD = 3 + 9 = 12 см, а верхнее основание ВС = НК = 6 см, высота же ВН = 3 см. Подставим в формулу для вычисления площади трапеции все эти данные и получим S = ½ (6 + 12)·3 = 27 см2.