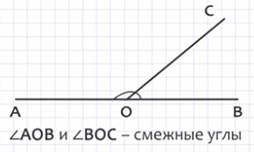
Рассмотрим развернутый угол АОВ, величина которого равна 180°. Проведем из вершины угла О луч ОС. Этот луч разделил развернутый угол на два угла АОС и ВОС. Такие углы называются смежными.

Определение: два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.

Так как лучи ОА и ОВ образуют развернутый угол, то ∠АОС + ∠ВОС = ∠АОВ = 180°.

Значит, сумма смежных углов равна 180°. Запомним это важное свойство.

Предположим, что ученику предложили построить угол, равный данному углу АОВ, только с помощью линейки и карандаша. Он поступил так: построил лучи ОС и ОD, как продолжение соответственно лучам ОВ и ОА, и заявил, что угол СОD= углу АОВ. Прав ли он? Докажем, что он прав.

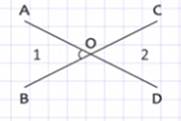
Чтобы установить равенство углов СОD и АОВ, т.е. углов 1 и 2, докажем, что их градусные меры равны. Угол 1 и угол DОВ смежные, значит, их сумма равна 180° (∠1 + ∠DОВ = 180°). Аналогично, угол 2 и угол ДОВ смежные, значит, и их сумма равна 180° (∠2 + ∠DОВ = 180°).

Из полученных равенств выразим угол 1 и угол 2, получаем:

∠1 = 180° – ∠DOВ,

∠2 = 180° – ∠DOВ.

Таким образом, градусные меры углов 1 и 2, т.е. углов СОD и АОВ равны. Ученик оказался прав. Эти углы называются вертикальными.

Определение: два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Запомним важное свойство вертикальных углов: вертикальные углы равны.

В жизни вы не раз встречались с четырьмя неразвернутыми углами, которые образуются при пересечении прямых. Выясним, какими углами окажутся все эти углы, если один из них будет прямым. Как называют в этом случае пересекающиеся прямые?

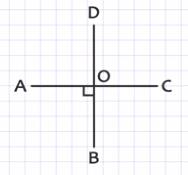
Построим прямой угол АОВ. Проведем лучи ОС и ОD, как продолжение лучам ОА и ОВ соответственно, получим две пересекающиеся прямые АС и ВD и четыре угла АОВ, АОD, СОD, СОВ. Угол АОВ равен углу ДОС как вертикальные. Так как угол АОВ = 90°, то и угол СОD= 90°, то есть прямой, тогда смежные углы СОВ и АОD также прямые (т.к. сумма смежных углов равна 180°). Таким образом, при пересечении двух прямых образовались четыре прямых угла. Эти прямые называются перпендикулярными.

Определение: две пересекающие прямые называются перпендикулярными(или взаимно перпендикулярными), если они образуют четыре прямых угла.

О таких прямых также говорят, что они пересекаются под прямым углом. На чертеже прямой угол отмечают квадратом.

Перпендикулярность прямых записывается так: АС⊥ВD, читается: «прямая АС перпендикулярна к прямой ВD».

Отметим важное утверждение: две прямые, перпендикулярные к третьей, не пересекаются.

Для проведения перпендикулярных прямых используют чертежный угольник и линейку.

В геодезии для построения прямых углов используют прибор теодолит.

Рассмотрим задачу.

Задача: Один из смежных углов на 16° больше другого. Найти величину каждого угла.

Решение:

Пусть меньший угол СОВ = х градусов, тогда угол АОС = х + 16°. Углы АОС и ВОС – смежные, значит, их сумма равна 180°.

Получаем: х + х + 16° = 180°

Решая это уравнение, находим неизвестное: х = 82°. Значит, угол СОВ = 82°, а угол АОС = 82° + 16° = 98°.

Ответ: угол ВОС = 82°, угол АОС = 98°.