Задача 1: Строительный блок массой М = 20 кг лежит на горизонтальной плоскости. Коэффициент трения покоя между блоком и плоскостью равен m = 0.1. Определить силу, которую необходимо приложить к блоку под углом α = 300 к горизонту, чтобы его сдвинуть.

Решение:

Запишем краткую запись. Нарисуем рисунки, отражающие условие задачи.

Рассмотрим силы, действующие на блок(рис. 1):

Так как силы – векторные величины, мы можем параллельным переносом сместить их в центр тяжести блока (рис. 2). Свяжем начало отсчета с центром тяжести блока. Запишем II закон Ньютона в векторной форме:

Спроецируем это уравнение на оси координат OX и OY:

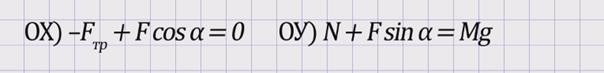
Решим систему полученных уравнений. Из проекции на ось ОУ) определим N(3)

Блок начинает скользить по поверхности в том случае, когда модуль силы трения покоя приобретает максимальное значение

С учетом формулы (3):

Подставив уравнение (4) в проекцию на ось ОХ), получим формулу для определения силы, которую нужно приложить к блоку, чтобы сдвинуть его с места:

Ответ: Чтобы сдвинуть с места строительный блок, к нему нужно приложить силу

F= 21,4Н под углом α = 300 .

Задача 2: Автомобиль, развивая силу тяги F = 3кН, поднимается в гору с уклоном

h/l = 0.2 с постоянной скоростью. Определить массу автомобиля, если он спускается при выключенном двигателе с той же скоростью.

Решение: Запишем краткую запись и переведем имеющиеся числовые данные в систему СИ. Нарисуем рисунки, отражающие условие задачи.

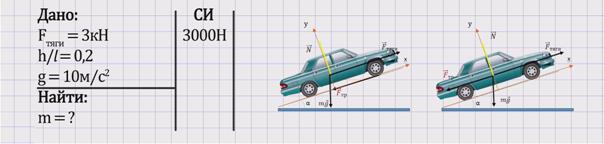
Изобразим на рисунке силы, действующие на автомобиль:

– сила тяги двигателя,

– сила трения,

– сила тяжести,

– сила реакции опоры

(где – сила реакции передней пары колес, – сила реакции задней пары колес).

Так как силы – векторные величины, мы можем параллельным переносом сместить их в центр тяжести автомобиля, с которым свяжем начало отсчета. Запишем II закон Ньютона для движения автомобиля вдоль наклонной плоскости в векторной форме (1):

Запишем второй закон Ньютона (1) в проекциях на оси координат OX и OY с учетом того, что автомобиль поднимается в гору c постоянной скоростью

Из уравнений (2) с учетом

получим формулу для силы тяги двигателя автомобиля (3)

При спуске двигатель автомобиля отключен, Fтяги = 0, сила трения теперь направлена вверх вдоль наклонной плоскости (рис. 5).

Второй закон Ньютона в проекциях на оси ОХ и ОУ имеет вид:

Из системы уравнений (4) следует, что

Откуда (5)

Подставляя формулу (5) в выражение для силы тяги (3), получим (6)

Согласно рисунку

Масса автомобиля:

Ответ: Масса автомобиля 1,5·103 кг .

Задача 3. Автомобиль движется по окружности радиусом R= 100 м со скоростью

u = 72 км/час, при превышении ,которой его «занесет». Найдите минимальный коэффициент трения, при котором «заноса» не будет.

Решение: Запишем краткую запись и переведем имеющиеся числовые данные в систему СИ. Нарисуем рисунок, отражающий условие задачи.

Спроецируем второй закон Ньютона (1) на оси координат OX и OY:

По определению с учетом уравнения (3) получим формулу для силы трения автомобиля о дорогу (4)

Приравнивая выражения для силы трения из уравнений (2) и (4), имеем

Ответ: Минимальный коэффициент трения, при котором «заноса» автомобиля при движении по окружности не будет, m = 0,4.