Задача 1:

Мотор автомобиля развивает силу тяги 1000 Н.

С какой скоростью будет ехать автомобиль через минуту после начала движения по льду, если его масса 1 т?

Решение:

Запишем краткую запись и переведем имеющиеся числовые данные в систему СИ:

Изобразим на рисунке силы, действующие на автомобиль:

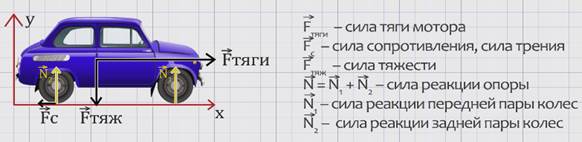
Так как силы – векторные величины, мы можем параллельным переносом сместить их в одну точку, называемую центром тяжести тела.

(Центром тяжести тела называется геометрическая точка, неизменно связанная с твёрдым телом, через которую проходит равнодействующая всех сил тяжести, действующих на частицы этого тела при любом положении последнего в пространстве).

Запишем II закон Ньютона:

Свяжем систему отсчета с местом старта.

Спроецируем уравнение на оси координат OX и OY:

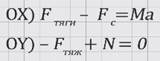
Автомобиль движется вдоль ровной поверхности (по крайней мере, о кочках ничего не говорится), сила тяжести автомобиля уравновешена силой реакции опоры (Земли). Поэтому в проекции уравнения на ось OY справа стоит 0, т.е. проекция равнодействующей силы

на ось OY равна нулю.

В условии задачи сказано: «…движения по льду».

Из этих слов следует, что мы можем пренебречь величиной силы трения.

В таком случае уравнение второго закона Ньютона в проекции на ось ОХ примет вид:

откуда ускорение:

Вспоминаем определение среднего ускорения:

Из условия задачи:

«через минуту после начала движения» – следует, что

Формула для ускорения получается:

Откуда выразим конечную скорость:

Ответ:

Через минуту после начала движения автомобиль будет ехать со скоростью

Предположим теперь, что наша дорога скользкая, но не ровная.

Оценим, с какой скорость автомобиль приземлится после преодоления ухаба высотой 20 см.

Задача 2:

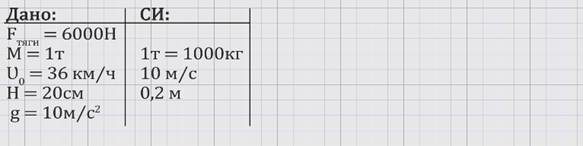
С какой скоростью приземлится автомобиль после преодоления ледяной горки высотой 20 см, если до препятствия он двигался равномерно и прямолинейно со скоростью 36 км/ч по скользкой дороге. Масса автомобиля 1 т, мотор автомобиля развивает силу тяги 6000 Н.

Решение:

Изобразим на рисунке силы, действующие на автомобиль:

Запишем II закон Ньютона:

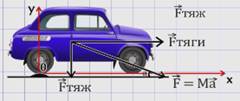
Свяжем систему отсчета с вершиной ухаба.

В момент падения сила тяжести не уравновешена силой реакции опоры, опоры нет, поэтому

Согласно условию задачи по-прежнему пренебрегаем трением.

Равнодействующая сила в данном случае направлена под углом а к горизонту.

Спроецируем уравнение на оси координат OX и OY:

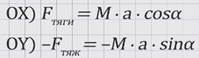
Откуда найдем ускорение

Если поделить уравнение 2 на уравнение 1, можно определить угол а:

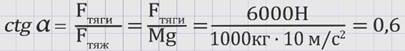
В таком случае

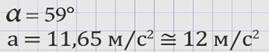
Это достаточно грубое округление продиктовано тем, что мы взяли ускорение свободного падения 10 м/с2 вместо 9,8 м/с2 для удобства.

Высота достаточно мала, чтобы машина не совершила вращения, т.е. будем считать, что она совершает поступательное движение по параболе и падает одновременно на 4 колеса параллельно дороге.

Скорость тела при равноускоренном движении изменяется по закону:

Спроектируем скорость на оси координат:

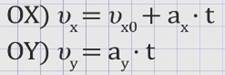
где

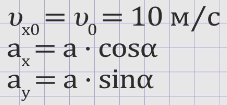
Время определим из кинематического уравнения движения по оси OY:

Когда машина приземлится, её координата в выбранной системе отсчета будет – h, тогда время полета

Сделаем предварительные преобразования конечной скорости, чтобы допустить минимальную погрешность:

Для сравнения: если мы воспользуемся формулой (6) скорость v = 11,14 м/с = 11 м/с.

Т.е. при решении по действиям возникла погрешность конечного результата 1 м/с, которой мы не можем пренебречь с помощью округления результата!

Решение по действиям может привести к печальным последствиям особенно в тестах, когда вы решили задачу верно, но выбрали неверный ответ.

Ответ: v = 12 м/с.

Важно запомнить:

Этапы решения задач:

1.Краткая запись. Выписать данные из условия задачи, перевести численные значения в систему СИ. Или выписать справочные данные при необходимости.

2.Рисунок. При построении рисунка мы представляем себе реальную ситуацию, какие силы действуют на тело, каков характер движения тела. Рекомендуется сделать 2 рисунка: на первом рисунке указать силы там, где они приложены, на втором рисунке сместить все силы в центр тяжести для удобства математических расчетов. На рисунке также нужно отметить направление скорости и ускорения, если тело движется.

3.Решение.

a)Записать 2 закон Ньютона в векторной форме.

b)Выбрать систему отсчета.

c)Спроецировать уравнение 2 закона Ньютона на оси выбранной системы координат.

d)По возможности упростить полученную в пункте В) систему уравнений, используя условие задачи.

e)Произвести математические преобразования, получить ответ.

f)Проверить размерность полученного результата.

g)Оценить реальность полученного результата, записать ответ.