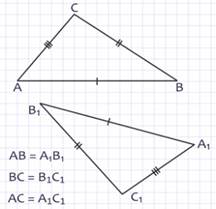
Рассмотрим два треугольника АВС и А1В1С1, у которых все соответствующие стороны равны, то есть АВ = А1В1, ВС = В1С1, АС = А1С1. Ответим на вопрос: равны ли эти треугольники? Ответ дает нам третий признак равенства треугольников.
Теорема:Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Докажем это утверждение.
Дано: треугольники АВС и А1В1С1, у которых АВ = А1В1, ВС = В1С1, АС = А1С1.
Доказать: треугольники АВС и А1В1С1 равны.
Доказательство: Приложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершина А совместилась с вершиной А1, вершина В – с вершиной В1 , а вершины С и С1 находились по разные стороны от прямой А1В1. Здесь возможны три случая расположения луча СС1:
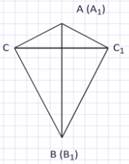
1 случай – луч СС1 проходит внутри угла В1С1А1
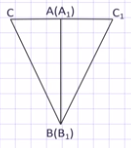
2 случай – луч СС1 совпадает с одной из сторон угла В1С1А1
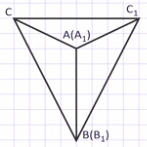
3 случай – луч СС1 проходит вне угла В1С1А1
Рассмотрим доказательство третьего случая. (Доказательство первых двух случаев рассмотрите самостоятельно).
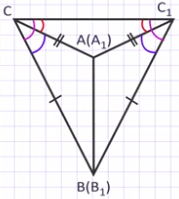
Треугольник В1С1С – равнобедренный с основанием С1С, так как ВС = В1С1 по условию теоремы. Угол В1С1С = углу В1СС1 как углы при основании равнобедренного треугольника. Треугольник А1С1С – равнобедренный с основанием С1С, так как АС = А1С1 по условию теоремы. Угол А1С1С = углу А1СС1, как углы при основании равнобедренного треугольника. Угол В1С1А1 = углу ВСА, как разность равных углов.
Тогда треугольники АВС и А1В1С1 равны по двум сторонам (ВС = В1С1, АС = А1С1) и углу между ними (угол ВСА = углу В1С1А1).
Теорема доказана.
Третий признак равенства треугольников можно назвать признаком равенства треугольников по трем сторонам.

Треугольник – жесткая фигура. В нем нельзя изменить ни один угол, ни одну сторону. Если бы удалось изменить угол или длину стороны треугольника, то мы получили бы уже новый треугольник, неравный первоначальному. Это свойство – жесткость треугольника – используется на практике. Например, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку.
Мы доказали третий признак равенства треугольников, рассмотрим задачу на его применение.
Задача: На отрезке АС как на основании построены по разные стороны от него два равнобедренных треугольника АСВ и АDС. Докажите, что ВD перпендикулярна АС.
Дано: треугольникиАСВ и АDС – равнобедренные, АС – их общее основание.
Доказать: ВD перпендикулярна АС.
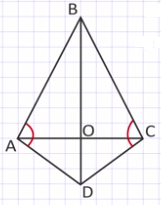
Доказательство: Треугольник АВD равен треугольнику СВD по третьему признаку равенства треугольников: АВ=ВС, АD=СD как боковые стороны равнобедренных треугольников АСВ и АDС, ВD - сторона общая. Так как треугольник АВD равен треугольнику СВD, то угол АВD равен углу СВD, а это значит, что ВD – биссектриса угла АВС. ВО – биссектриса, проведенная из вершины равнобедренного треугольника АВС к его основанию АС, а по свойству биссектрисы равнобедренного треугольника она является и высотой. Так как ВО – высота треугольника АВС, то ВО перпендикулярна АС, а значит, ВD перпендикулярна АС.
Что и требовалось доказать.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!