Отметим три точки, не лежащие на одной прямой, и соединим их отрезками. Получим геометрическую фигуру, которая называется треугольником.Точки называются вершинами треугольника, а отрезки –сторонамитреугольника. Любой треугольник имеет три угла и три стороны.
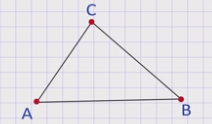
На рисунке изображен треугольник АВС, точки А, В, С являются вершинами треугольника, отрезки АВ, ВС, АС – стороны треугольника. Данный треугольник можно обозначить иначе: треугольник ВСА или САВ, то есть, назвав вершины треугольника в любой другой последовательности. Углы АВС, ВСА и САВ называются угламитреугольника. Их еще можно обозначать одной буквой: угол А, угол В, угол С. Углы и стороны треугольника называют его основными элементами.
Сумма длин трех сторон треугольника называется периметром треугольника.
Об одном угле треугольника можно сказать, что он лежит между сторонами, а о двух углах – что они прилежат к одной стороне. Так, угол А лежит между сторонами АВ и АС, а угол С – между сторонами АС и СВ. Углы А и С прилежат к стороне АС, а углы В и А прилежат к стороне АВ. Кроме того, употребляются выражения: «Угол лежит против стороны», «Сторона лежит против угла». Например, угол А лежит против стороны ВС, а сторона АВ лежит против угла С.
Два треугольника называются равными, если их можно совместить наложением.
В совпадающих треугольниках равны все соответствующие элементы, то есть равны соответствующие стороны и углы.
Запись ∆ АВС = ∆ А1В1С1понимается так: ∠ А = ∠ А1, ∠ В = ∠ В1, ∠ С = ∠ С1, АВ = А1В1, ВС = В1С1, АС = А1С1.
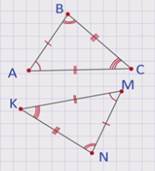
На чертеже равные углы треугольников отмечают одинаковым числом дуг, а равные стороны – одинаковым числом черточек.
На рисунке треугольник АВС равен треугольнику МNК. По тому, как отмечены углы и стороны в этих треугольниках, можно заключить, что ∠ А = ∠ М, ∠ В = ∠ N, ∠ С = ∠ К, АВ = МN, ВС = NК, АС = МК.
Отметим, что в равных треугольниках против соответственно равных сторон лежат равные углы и против соответственно равных углов лежат равные стороны.
Чтобы установить равенство треугольников без наложения их друг на друга, вовсе необязательно устанавливать равенство всех шести соответствующих элементов – трех углов и трех сторон. Оказывается, достаточно установить равенство некоторых из них. О том, какие именно элементы нужно сравнивать, нам расскажут признаки равенства треугольников.
В математике правильность утверждения устанавливается путем рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
Рассмотрим первый признак равенства треугольников.
Теорема:Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Докажем это утверждение.
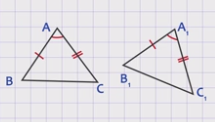
Дано: треугольники АВС и А1В1С1, сторона АВ = стороне А1В1, сторона АС = стороне А1С1, угол А = углу А1.
Доказать: треугольники АВС и А1В1С1 равны.
Доказательство: Так как угол А = углу А1, то треугольник АВС можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. А так так отрезок АВ = отрезку А1В1 и отрезок АС = отрезку А1С1, то соответствующие стороны совместятся и, в частности, вершины В и С треугольника АВС совместятся соответственно с вершинами В1 и С1 треугольника А1В1С1. Следовательно, совместятся стороны ВС и В1С1. Таким образом, треугольники АВС и А1В1С1 полностью совместятся, значит, эти треугольники равны. Теорема доказана.
Рассмотрим задачу.
Задача: На рисунке АД = СД, угол 1 = углу 2. Доказать, что треугольник АВД равен треугольнику СВД. Найти ВС и СД, если АВ=15 см, АД= 12 см.
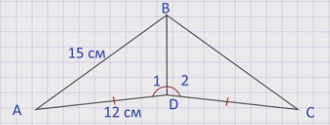
Решение:
По условию задачи:
во-первых, сторона АД = стороне СД
во-вторых, угол 1 = углу 2
и в-третьих, у данных треугольников сторона ВД – общая.
Треугольники АВД и СВД равны по первому признаку равенства треугольников, а именно, по двум сторонам и углу между ними. Что и требовалось доказать.
Так как треугольники равны, то все соответствующие стороны этих треугольников равны.
АВ = ВС = 15 см, АД = СД = 12 см.
Ответ: ВС=15 см, СД= 12 см.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!