На этом занятии мы узнаем, какой отрезок в геометрии называют перпендикуляром, проведенным из данной точки к прямой, выясним, что подразумевается под понятиями медиана, биссектриса и высота треугольника и сколько их в треугольнике.

Рассмотрим прямую m, отметим точку А, не принадлежащую прямой m. Так как прямая состоит из точек, то, соединив каждую точку прямой с точкой А, получим бесконечно много отрезков разной длины – АВ, АС, АК, АD. Эти длины являются расстояниями от точки А до точек прямой. Но среди них есть отрезок, который имеет наименьшую длину. Это отрезок АD. Точка D прямой m самая близкая к точке А. Обратите внимание – АD и m перпендикулярны.

Отрезок АD называется перпендикуляром, проведенным из точки А к прямой m, если прямые АD и m перпендикулярны.

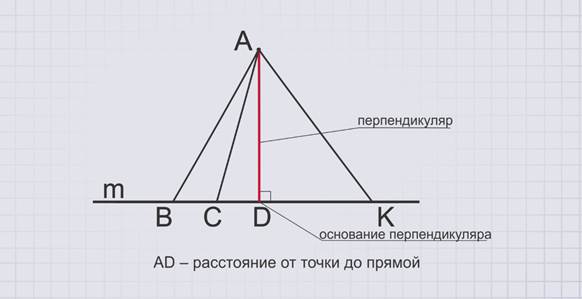
Точка D называется основаниемперпендикуляра. Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.

Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Дано: m – прямая и точка А, не принадлежащая этой прямой.

Доказать:

1.из точки А к прямой m можно провести перпендикуляр;

2.точки А к прямой m можно провести единственный перпендикуляр.

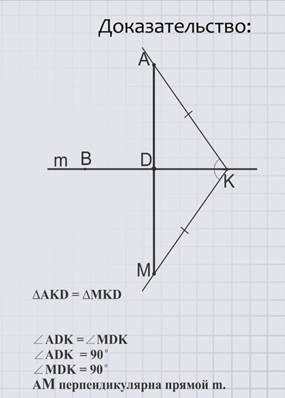
Доказательство:

Отметим на прямой m какую-нибудь точку К и проведем луч КА, получили угол ВКА. Отложим от луча ВК угол ВКМ, равный углу ВКА. На луче КМ отложим отрезок КМ=КА. Проведем отрезок АМ. Он пересечет прямую m в точке D. Получили, что треугольник АКD = треугольнику МКD (по первому признаку равенства треугольников). Значит, угол АDК = углу МDК, но эти углы смежные, значит, каждый из них прямой. Итак, АМ перпендикулярна прямой m.

Докажем теперь, что из точки А можно провести единственный перпендикуляр.

Если предположить, что существует ещё один перпендикуляр к прямой m, то получим, что две перпендикулярные прямые пересекаются в точке. А это противоречит утверждению: две прямые, перпендикулярные к третьей, не пересекаются. Итак, из точки А к прямой m можно провести единственный перпендикуляр. Теорема доказана.