Треугольник - одна из самых распространенных фигур в геометрии. Вениамин Фёдорович Каган, русский математик ХХ века, однажды сказал: «Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике…» действительно одна из важнейших теорем геометрии гласит

Теорема: Сумма углов в треугольнике равна 180 градусов.

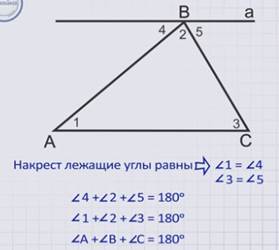
Докажем эту теорему. Для этого возьмем произвольный треугольник АВС. Через вершину В проведем прямую а параллельную стороне треугольника АС. Пронумеруем получившиеся углы: 1,2,3 номера углов при вершинах А, В и С соответственно, углы 4 и 5 образованы прямой а и сторонами АВ и ВС треугольника. Первый и четвертый углы являются накрест лежащими при пересечении параллельных прямых АС и а секущей АВ. Согласно теореме о накрест лежащих углах, они равны, то есть первый угол равен четвертому. Аналогично третий угол равен пятому, так как являются накрест лежащими при пересечении параллельных а и АС секущей ВС.

Сумма углов 4, 2 и 5 представляют собой развернутый угол с вершиной В, а он, как известно, равен 180 градусам. Тогда, исходя из равенства углов 1 и 4, 3 и 5, получаем, что сумма первого, второго и третьего углов равна 180 градусам. То есть угол А плюс угол В плюс угол С равно 180 градусов. 

Что и требовалось доказать.

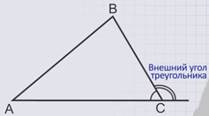
А теперь продлим сторону АС треугольника АВС и рассмотрим смежный угол угла С, такой угол называется – внешним углом треугольника.

Поскольку смежные углы составляют развернутый угол, их сумма равна 180 градусам, тогда внешний угол треугольника равен 180 градусов минус угол С. А нам теперь известно, что сумма углов треугольника равна 180 градусам, и из этой теоремы следует, что 180 градусов минус угол С - это сумма углов А и В. Значит, величина внешнего угла треугольника равна сумме двух углов треугольника не смежных с ним.

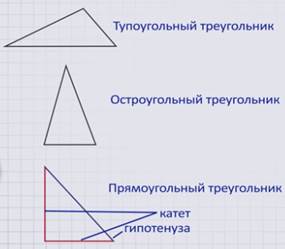
Представим, что в треугольнике один угол 90 градусов, тогда, согласно теореме о сумме углов в треугольнике, сумма оставшихся двух углов должна быть равна 180 - 90 = 90 градусам, из чего следует, что оставшиеся углы острые. Если же в треугольнике есть тупой угол, то есть больше 90 градусов, то оставшиеся два углы в сумме должны быть меньше 90 градусов и, значит, также будут острыми. Таким образом, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой. Поэтому в зависимости от вида угла рассматриваемый треугольник может быть:тупоугольным, если среди его углов есть тупой угол, остроугольным, если все три угла треугольника острые, или прямоугольным, если в треугольнике есть угол, равный 90 градусам.

В прямоугольном треугольнике стороны, расположенные друг к другу под прямым углом, называют катетами, а сторону, расположенную напротив угла в 90 градусов, гипотенузой.

Итак, сумма углов в треугольнике равна 180 градусам. 

Угол смежный с углом при вершине треугольника называется внешним углом треугольника и равен сумме двух углов треугольника не смежных с ним. 

Треугольники могут быть трёх видов: остроугольные, тупоугольные и прямоугольные.