Измерение расстояния между двумя объектами - наиболее частый вид измерения, который мы встречаем в повседневной жизни. Например, необходимо измерить ширину комнаты для определения количества рулонов обоев, а для этого надо измерить расстояние между двумя параллельными прямыми. В геометрии существуют определения расстояния между точкой и прямой и расстояния между параллельными прямыми.

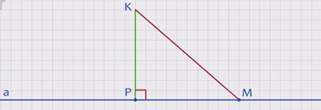
Пусть КР – перпендикуляр, проведенный из точки К к прямой а. Возьмем любую точку М прямой а, не совпадающую с точкой Р. Проведем отрезок КМ. Этот отрезок называется наклонной, проведенной из точки К к прямой а. В прямоугольном треугольнике КРМ гипотенуза КМ наибольшая сторона, значит, больше катета КР. Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.

Длина перпендикуляра, проведенного из точки к прямой, называетсярасстоянием от этой точки до прямой.

Также расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой.

Отметим, что расстояние от точки до прямой удобнее измерять при помощи инструмента «треугольник».

А как в геометрии определено понятие расстояния между параллельными прямыми? При рассмотрении этого вопроса важно знать следующее свойство параллельных прямых: все точки каждой из двух параллельных прямых равноудалены от другой прямой.

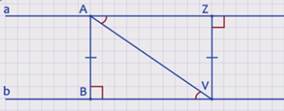
Докажем это утверждение. Рассмотрим параллельные прямые а и b. Отметим на прямой а точку А и проведем перпендикуляр АВ к прямой b. Докажем, что расстояние от любой точки Z прямой а до прямой b равно АВ.

Проведем из точки Z перпендикуляр ZV к прямой b. Так как ZV перпендикулярно b, то ZV перпендикулярно а. Соединим точки А и V. В прямоугольных треугольниках АВV и VZА угол VАZ равен углу АVВ, как накрест лежащие углы при пересечении параллельных прямых а и b секущей АV, также в этих треугольниках общая гипотенуза АV, значит, рассматриваемые треугольники равны по гипотенузе и острому углу. Следовательно, ZV равно АВ. Итак, любая точка Z прямой а находится на расстоянии АВ от прямой b. Очевидно, что все точки прямой b находятся на том же расстоянии от прямой а, что и требовалось доказать.

Также верно утверждение обратное доказанному: все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой параллельной данной.

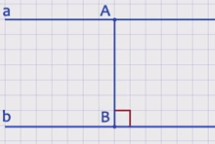
Вернемся к понятию расстояния между параллельными прямыми: расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.

Итак,

-перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой;

-длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой;

-все точки каждой из двух параллельных прямых равноудалены от другой прямой;

-все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной;

-расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.