На этом уроке вы узнаете, что такое угол, как его правильно обозначать, познакомитесь с понятиями развернутого и прямого углов, а также научитесь работать с чертежным треугольником.

Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят – вершиной угла.

Для обозначения угла имеется общепринятый символ, предложенный в 1634 году французским математиком Пьером Эригоном.

В математических выражениях углы часто обозначают строчными греческими буквами:

Также часто угол обозначают тремя точками, например:

В такой записи B — это вершина, а A и C — точки, лежащие на разных сторонах угла. Т.е. при записи угла в середине пишут букву, обозначающую его вершину.

Угол можно обозначить и одной буквой – названием его вершины. Например:

На чертежах углы отмечаются небольшими одинарными, двойными или тройными дужками, проходящими по внутренней области угла с центрами в вершине угла.

Равенство углов может отмечаться одинаковой кратностью дужек.

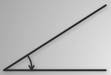
Если необходимо указать направление отсчёта угла, оно отмечается стрелкой на дужке.

Как и все геометрические фигуры, углы сравниваются с помощью наложения.

Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.

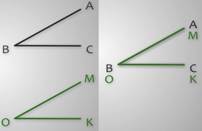
Например, угол АВС равен углу МОК.

На рисунке показано, что эти углы полностью совпадают при наложении. 

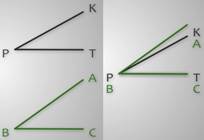
Или же, угол АВС больше угла КРТ.

На рисунке показано, что эти углы при наложении не совпали, и угол АВС оказался больше угла КРТ.

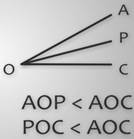
Другая ситуация: из вершины угла АОС проведен луч ОР.

Он разбивает угол АОС на два угла – АОР и РОС.

Каждый из этих углов меньше исходного угла АОС.

Пишут таким образом:

угол АОР меньше угла АОС и угол РОС меньше угла АОС.

Давайте проведем прямую и отметим на ней точку. Получилось два луча, которые будем называть дополнительными. Два дополнительных друг другу луча образуют развернутый угол.

Давайте для наглядности представим часы: когда они показывают ровно шесть часов, то часовая и минутная стрелки образуют развернутый угол.

Другой пример, угол АОВ – развернутый, так как лучи ОА и ОВ являются дополнительными, т.е. образуют прямую.

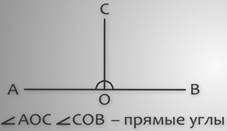
Теперь, давайте проведем луч ОС так, чтобы он разделил развернутый угол АОВ на два равных угла АОС и СОВ. Каждый из этих углов равен половине угла АОВ, т.е. половине развернутого угла.

Такие углы называют прямыми.

Значит угол АОС и угол СОВ – прямые углы.

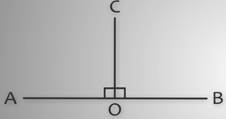
Прямые углы отмечаются не дужками, как другие углы, а двумя соединёнными равными отрезками, расположенными таким образом, что вместе со сторонами они образуют небольшой квадрат, одна из вершин которого совпадает с вершиной угла.

Для построения прямого угла пользуются чертежным треугольником или линейкой. Чтобы построить прямой угол, одной из сторон которого является луч ОА, надо:

1)расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА.

2)провести вдоль второй стороны треугольника луч ОВ.

В результате получили прямой угол АОВ.

Таким образом, в этом уроке Вы познакомились с понятием угла, узнали что такое развернутый угол и его половина – прямой угол. Кроме того, научились выполнять построение углов.