В этом уроке познакомимся с равносоставленными и равновеликими фигурами.

Возьмем два одинаковых прямоугольных треугольника.

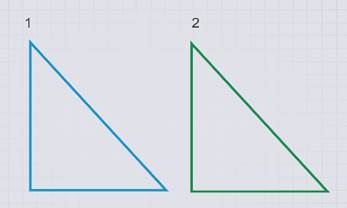
Какие фигуры можно из них составить?

Можно составить прямоугольник, треугольник.

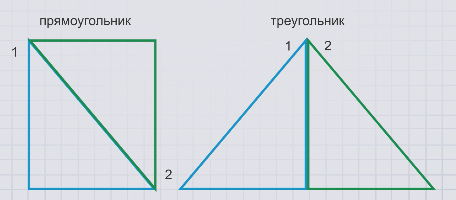
Для составления прямоугольника и треугольника использовали одинаковый набор фигур, поэтому полученные фигуры называют равносоставленными.

Дадим определение.

Равносоставленные фигуры – это те, которые можно составить (способом приложения) из одного и того же набора плоских фигур, при этом все фигуры набора должны участвовать в составлении. Из одного набора плоских фигур можно составить несколько новых фигур, и все они будут равносоставленными, если при составлении мы использовали все фигуры набора.

Так как равносоставленные фигуры состоят из одних и тех же фигур, можно заключить, что они имеют одинаковую площадь.

Докажем это.

Начертим прямоугольник со сторонами 3 и 5 см.

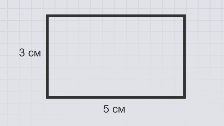
Площадь данного прямоугольника равна произведению 3 и 5.

3 умножить на 5, равно 15 см2.

Вырежем прямоугольник.

Проведем в нем диагональ и разрежем по ней прямоугольник на два одинаковых треугольника.

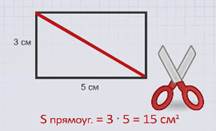
Сложим из полученных фигур новую фигуру – треугольник.

Полученный треугольник и прямоугольник – равносоставленные фигуры, так как состоят из одного и того же набора плоских фигур.

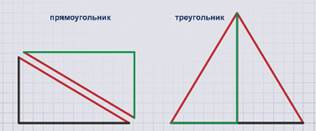
Изначально у нас был прямоугольник, площадь которого не изменилась после того как мы разрезали его на два треугольника, из которых потом составили треугольник.

Т.е. можно сделать вывод, что данный прямоугольник и треугольник, составленный из частей прямоугольника, имеют одинаковую площадь.

Фигуры, имеющие одинаковую площадь, называются равновеликими.

Все равносоставленные фигуры являются равновеликими.

Выполним практическое задание.

Даны две фигуры: четырехугольник и прямоугольник.

Докажите, что они равновеликие.

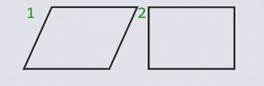
Разделим четырехугольник на части, из которых можно сложить данный прямоугольник: 2 треугольника и квадрат.

Переложим один треугольник так, чтобы получился прямоугольник.

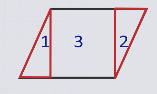
Новый прямоугольник и данный прямоугольник при наложении совпадают.

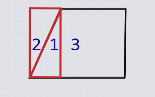
Прямоугольник и четырехугольник состоят из одного и того же набора фигур, следовательно, четырехугольник и прямоугольник являются фигурами равносоставленными, а значит, равновеликими.

Найдем площадь квадрата со стороной 4 см и прямоугольника со сторонами 8 и 2 см.

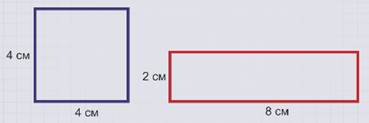
Площадь квадрата равна произведению 4 и 4, равно 16 см2, площадь прямоугольника равна произведению 8 и 2, равно 16 см2.

Данные квадрат и прямоугольник – равновеликие фигуры, так как площади их равны.

Заметим, что не все равновеликие фигуры обязательно должны быть равносоставленными.

Выполним практическое задание на нахождение площади.

Возьмем квадрат со стороной 6 см. Разделим его на 4 одинаковых треугольника.

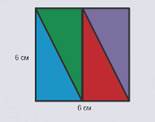
Чему равна площадь каждого треугольника?

Найдем сначала площадь квадрата: 6 ∙ 6 = 36 см2.

Квадрат составлен из 4 одинаковых треугольников.

Значит, площадь одного треугольника в 4 раза меньше площади квадрата.

36 : 4 = 9 см2.

Получили, что площадь каждого треугольника равна 9 см2.

В этом уроке вы познакомились с равносоставленными и равновеликими фигурами, а также решили несколько заданий по теме урока.