В этом уроке выясним, сколько общих точек могут иметь прямая и окружность в зависимости от их расположения, познакомимся с понятием секущая по отношению к окружности, рассмотрим решение задачи по теме урока.

Рассмотрим следующее взаимное расположение прямой и окружности: прямая проходит через центр окружности.

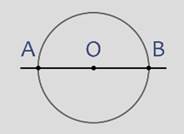
В этом случае прямая пересечет окружность в двух точках, эти точки являются концами диаметра окружности, лежащего на этой прямой.

Рассмотрим другой случай, когда прямая р не проходит через центр О окружности

радиуса r. Проведем перпендикуляр ОН к прямой р, обозначим длину перпендикуляра буквой d – это расстояние от центра О окружности до данной прямой р.

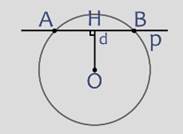
Взаимное расположение прямой и окружности зависит от соотношения между величинами d и r.

Рассмотрим все возможные варианты, их три: d меньше r, d и r равны, d больше r.

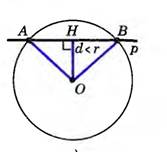
Рассмотрим первый вариант, когда расстояние от центра окружности до прямой меньше радиуса окружности (d < r).

На прямой р от точки Н отложим два отрезка АН и ВН одинаковой длины, равной корню квадратному разности квадратов r и d:

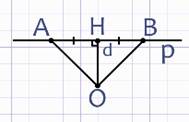
По теореме Пифагора из прямоугольных треугольников АОН и ВОН найдем ОА и ОВ:

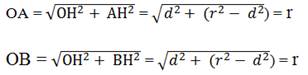
Получили, что ОА и ОВ равны радиусу окружности, следовательно, точки А и В лежат на этой окружности, а значит, являются общими точками прямой р и окружности.

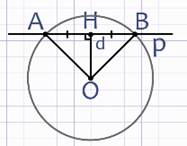
Докажем, что прямая р и окружность не имеют других общих точек.

Воспользуемся методом доказательства от противного.

Предположим, что они имеют еще одну общую точку С.

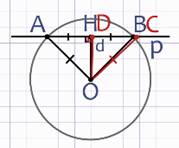
А значит, можно рассмотреть треугольник ОАС, который будет равнобедренным, а в равнобедренном треугольнике медиана ОD, проведенная к основанию АС, является высотой этого треугольника, следовательно, ОD перпендикулярна прямой р.

Отрезки ОD и ОН не совпадают, так как середина D отрезка АС не совпадает с точкой Н, которая является серединой отрезка АВ.

Получили, что из точки О проведены два перпендикуляра ОН и ОD к прямой р, что невозможно.

Таким образом, если расстояние от центра окружности до прямой меньше радиуса окружности (d < r), то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Рассмотрим второй вариант, когда расстояние от центра окружности до прямой равно радиусу окружности (d = r). В этом случае ОН = r, т.е. точка Н лежит на окружности и является общей точкой прямой и окружности.

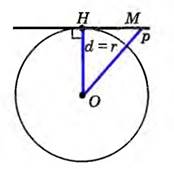
Прямая р и окружность не имеют других общих точек, так как для любой отличной от Н точки, например М, лежащей на прямой р, ОМ будет являться наклонной, а наклонная всегда больше перпендикуляра ОН, равного r (ОМ>ОН= r), следовательно, точка М не лежит на окружности.

Таким образом, если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.

Третий вариант, когда расстояние от центра окружности до прямой больше радиуса окружности (d > r). В этом случае ОН больше радиуса, поэтому для любой точки М прямой р ОМ > ОН > r, следовательно, точка М не лежит на окружности.

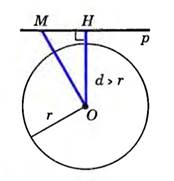
Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Решим задачу:

В прямоугольном треугольнике МЕК с прямым углом Е катеты равны 6 см и 8 см.

С центром в точке Е проведена окружность.

Каково взаимное расположение окружности и прямой МК, если радиус окружности равен 4,8 см?

Дано:

∆МЕК прямоугольный (∠Е= 90°)

МЕ = 6 см

ЕК = 8 см

окр. (Е, r), r = 4,8 см.

Определить:

взаимное расположение окружности и прямой МК.

Решение:

Расстояние от центра Е окружности до прямой МК равно высоте ЕН ∆МЕК.

Высоту ЕН вычислим через площадь треугольника ∆МЕК, которая равна половине произведения его основания на высоту:

Основание МК является гипотенузой, по теореме Пифагора:

С другой стороны, площадь этого прямоугольного треугольника равна половине произведения его катетов:

Таким образом, получаем:

Значит, радиус окружности и расстояние от центра окружности до прямой равны между собой, следовательно, окружность и прямая МК имею одну общую точку.

Итак, в этом уроке Вы рассмотрели возможные варианты взаимного расположения прямой и окружности, узнали, какую прямую называют секущей по отношению к окружности, а также рассмотрели решение задачи по теме урока.