В этом уроке узнаем, что подразумевается под понятием «описанная окружность», докажем теорему об окружности, описанной около треугольника, отметим некоторые свойства, а также решим задачу по теме урока.

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

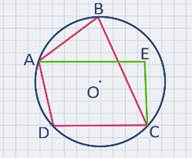
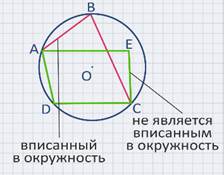
На рисунке изображена окружность, описанная около четырехугольника АВСD. Четырехугольник АВСD является вписанным в окружность, так как все его вершины лежат на окружности, а четырехугольник АЕСD не является вписанным в окружность, так как его вершина Е не лежит на данной окружности.

Докажем теорему об окружности, описанной около треугольника.

Теорема:

Около любого треугольника можно описать окружность.

Дано:

произвольный треугольник Δ АВС.

Доказать:

около треугольника ΔАВС можно описать окружность.

Доказательство:

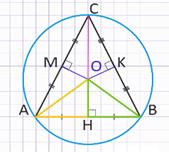
в треугольнике ΔАВС проведем серединные перпендикуляры ОН к стороне АВ, ОК к стороне ВС и ОМ к стороне АС, точка О – точка пересечения этих серединных перпендикуляров.

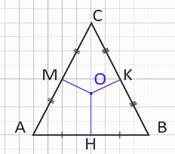
НКМИз точки О проведем отрезки АО, ВО, СО.

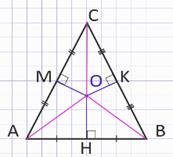
Рассмотрим прямоугольные треугольники ΔАОН и ΔВОН.

Так как ОН – общая сторона, АН = ВН по построению, то ΔАОН = ΔВОН (по двум катетам), следовательно, АО = ВО.

Аналогично из равенства прямоугольных треугольников ΔВОК и ΔСОК; ΔСОМ и ΔАОМ следует ВО = СО и СО = АО.

Значит, АО = ВО = СО.

Поэтому окружность с центром О и радиуса ОА проходит через все три вершины треугольника АВС и, значит, является описанной около треугольника.

Теорема доказана.

Важно отметить, что:

1) около треугольника можно описать только одну окружность;

2) в отличие от треугольника около четырехугольника не всегда можно описать окружность.

Те четырехугольники, около которых можно описать окружность, обладают замечательным свойством: в любом вписанном четырехугольнике сумма противоположных углов равна 180°.

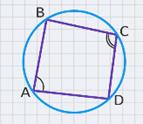
На рисунке углы А и С – вписанные углы.

По теореме о вписанном угле:

Сложим углы А и С, получим:

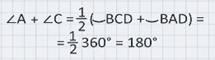
Верно и обратное утверждение: если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.

Рассмотрим решение задачи по теме урока.

Задача:

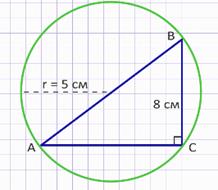
Прямоугольный треугольник АВС с прямым углом С вписан в окружность.

Найдите площадь треугольника АВС, если ВС = 8 см и радиус окружности, описанной около треугольника, равен 5 см.

Дано: треугольник АВС – прямоугольный, ВС = 8 см, окружность, описанная около треугольника АВС, с радиусом r = 5 см.

Найти:

площадь треугольника АВС.

Решение:

так как вписанный прямой угол С прямоугольного треугольника АВС равен половине дуги, на которую он опирается, то гипотенуза АВ треугольника является диаметром окружности, описанной около треугольника.

Тогда АВ = 2 r = 10 см.

Для вычисления площади треугольника надо вычислить катет АС.

Вычислим катет АС, применяя теорему Пифагора:

Тогда площадь треугольника будет равна:

В этом уроке Вы познакомились с понятием «описанная окружность», доказали теорему об окружности, описанной около треугольника, рассмотрели замечательное свойство углов четырехугольника вписанного в окружность и решили задачу по теме урока.