На этом уроке мы познакомимся с одним из часто используемых понятий геометрии «вписанная окружность», докажем теорему об окружности, вписанной в треугольник, отметим некоторые закономерности, связанные с новым понятием, а также решим задачу, используя полученные знания.

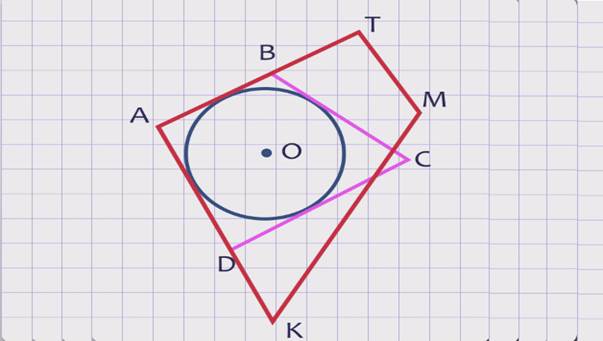
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

На рисунке все стороны четырехугольника АВСD касаются окружности с центром О, эта окружность является вписанной в данный четырехугольник, а сам четырехугольник АВСD описан около окружности. А четырехугольник АКМТ не является описанным около окружности с центром О, так как его стороны КМ и МТ не касаются этой окружности.

Докажем теорему об окружности, вписанной в треугольник.

Теорема: в любой треугольник можно вписать окружность.

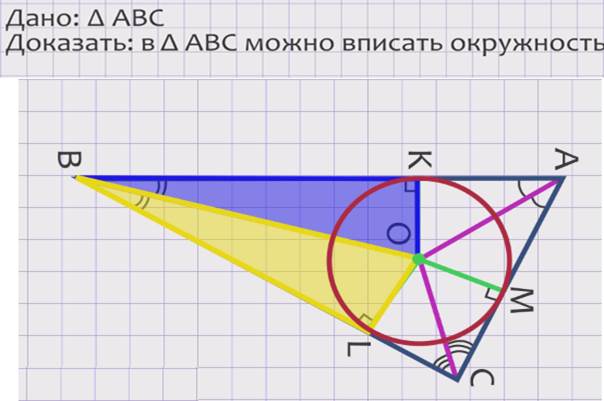
Доказательство: в треугольнике АВС проведем биссектрисы АО, ВО, СО, точка

О – точка пересечения этих биссектрис.

Из точки О проведем перпендикуляры к сторонам треугольника АВС: ОМ к стороне АС, ОК к стороне АВ, ОL к стороне ВС.

Рассмотрим прямоугольные треугольники КОВ и LОВ. Так как ОВ – общая сторона, углы КВО и LВО равны по построению, то Δ КОВ = ΔLОВ (по гипотенузе и острому углу), следовательно, КО = LО. Аналогично из равенства прямоугольных треугольников LОС и МОС, МОА и КОА имеем LО = МО и МО = КО и значит,

КО = LО = МО. Поэтому окружность с центром О радиуса ОК проходит через точки

К, L и М. Стороны треугольника ΔАВС касаются этой окружности в точках К, L, М, так как они перпендикуляры по построению к радиусам ОК, ОL и ОМ. Значит, окружность с центром в точке О радиуса ОК является вписанной в треугольник ΔАВС.

Теорема доказана.

Сделаем ряд замечаний.

Замечания:

1) в треугольник можно вписать только одну окружность;

2) не во всякий четырехугольник можно вписать окружность.

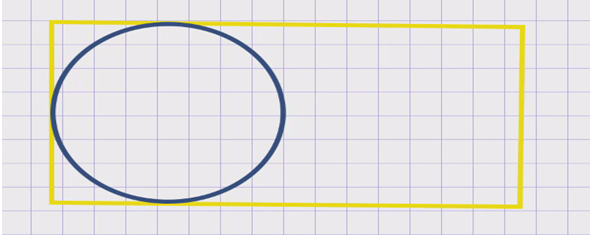
Например, в прямоугольник, у которого смежные стороны не равны, нельзя вписать окружность, так как окружность не будет касаться всех четырех его сторон.

Если же в четырехугольник можно вписать окружность, то его стороны обладают замечательным свойством: в любом описанном четырехугольнике суммы противоположных сторон равны.

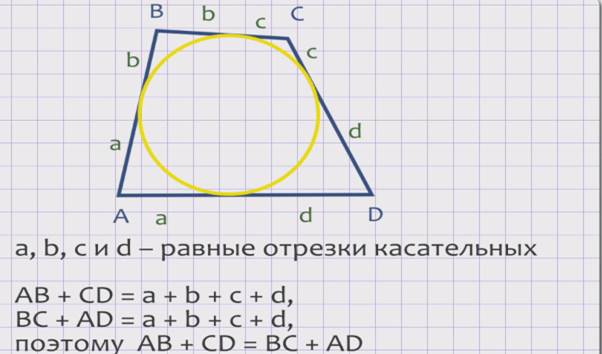
На рисунке буквами а, b, с и d отмечены равные отрезки касательных.

АВ + СD = а + b + с + d, ВС + АD = а + b + с + d, поэтому АВ + СD = ВС + АD.

Верно и обратное утверждение: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Рассмотрим решение задачи по теме урока.

Задача. Основание АС и высота ВН равнобедренного треугольника АВС соответственно равны

12 см и 8 см. Найдите радиус вписанной окружности.

Решение: известно, что в равнобедренном треугольнике высота является также биссектрисой и медианой. Так как треугольник АВС равнобедренный, то центр вписанной окружности – точка О – лежит на его высоте ВН. Радиус ОН = r, тогда

ВО = ВН – ОН = 8 – r. Так как ВН – медиана равнобедренного треугольника АВС, то

СН – половина основания АС, значит, СН = АС : 2 = 12 : 2 = 6 см.

Обозначим точку касания вписанной окружности и стороны ВС треугольника АВС через К, тогда отрезок ОК – радиус окружности, перпендикулярен стороне ВС. Рассмотрим прямоугольные треугольники НОС и СОК. Так как СО – общая гипотенуза, а ОН и ОК равны как радиусы окружности, то по гипотенузе и катету треугольники НОС и СОК равны, значит, СК = СН = 6 см.

Отсюда ВК = ВС – СК = 10 – 6 = 4 см. Рассмотрим прямоугольный треугольник ВОК и применим к нему теорему Пифагора: ВО2 = ОК2 + ВК2; получим уравнение

(8 – r)2 = r2 + 42 решим его и найдем, чему равен радиус r:

64 – 16r + r2 = r2+ 16; – 16r = 16 – 64; r = 3 см.

Ответ: радиус вписанной окружности равен 3 см.

На этом уроке мы познакомились с понятием «вписанная окружность», доказали теорему об окружности, вписанной в треугольник, рассмотрели замечательное свойство сторон четырехугольника описанного около окружности, а также решили задачу, используя полученные знания.