Вспомним, что такое система уравнений.
Система двух уравнений с двумя переменными – это записанные друг под другом два уравнения, объединённые фигурной скобкой. Решить систему – это значит найти такую пару чисел, которая будет являться решением и первого, и второго уравнения одновременно.
В этом уроке познакомимся с таким способом решения систем, как способподстановки.
Давайте рассмотрим систему уравнений:
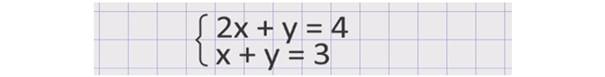
Можно решить эту систему графически. Для этого нам надо будет построить в одной системе координат графики каждого из уравнений, преобразовав их к виду:
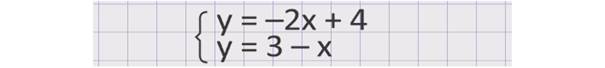
Затем найти координаты точки пересечения графиков, которые и будут являться решением системы. Но графический способ далеко не всегда удобен, т.к. отличается малой точностью, а то и вовсе недоступностью. Попробуем рассмотреть нашу систему повнимательнее. Теперь она имеет вид:
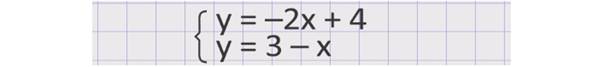
Можно заметить, что левые части уравнений равны, а значит, должны быть равны и правые. Тогда мы получим уравнение:
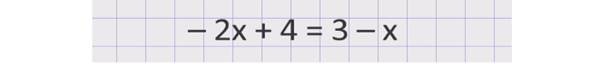
Это знакомое нам уравнение с одной переменной, которое мы решать умеем. Перенесём неизвестные слагаемые в левую часть, а известные – в правую, не забыв поменять знаки +,– при переносе. Получим:
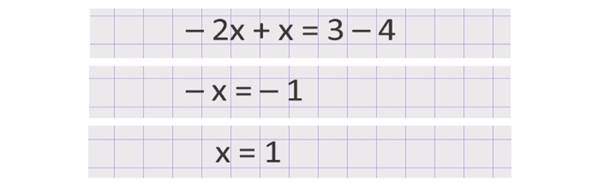
Теперь подставим найденное значение х в любое уравнение системы и найдём значение у. В нашей системе удобнее использовать второе уравнение у = 3 – х, после подстановки получим у = 2. А теперь проанализируем выполненную работу. Сначала мы в первом уравнении выразили переменную у через переменную х. Затем полученное выражение – 2х + 4 подставили во второе уравнение вместо переменной у. Потом решили полученное уравнение с одной переменной х и нашли ее значение. И в заключении использовали найденное значение х для нахождения другой переменной у. Тут возникает вопрос: а обязательно ли было выражать переменную у из обоих уравнений сразу? Конечно нет. Мы могли выразить одну переменную через другую только в одном уравнении системы и использовать его вместо соответствующей переменной во втором. Причём выразить можно любую переменную из любого уравнения. Здесь выбор зависит исключительно из удобства счёта. Подобный порядок действий математики назвали алгоритмом решения систем двух уравнений с двумя переменными методом подстановки.Вот как он выглядит.
1.Выразить одну из переменных через другую в одном из уравнений системы.
2.Подставить полученное выражение вместо соответствующей переменной в другое уравнение системы.
3.Решить полученное уравнение с одной переменной.
4.Найденное значение переменной подставить в выражение, полученное в пункте первом, и найти значение другой переменной.
5.Записать ответ в виде пары чисел, которые были найдены на третьем и четвертом шаге.
Давайте рассмотрим ещё один пример. Решить систему уравнений:
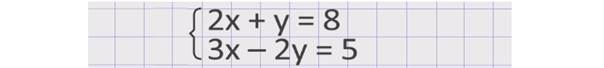
Здесь удобнее выразить переменную у из первого уравнения. Получим у = 8 – 2х. Полученное выражение надо подставить вместо у во второе уравнение. Получим:
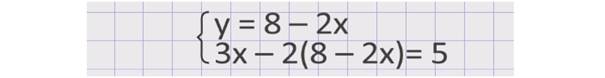
Выпишем это уравнение отдельно и решим его. Сначала раскроем скобки. Получим уравнение 3х – 16 + 4х = 5. Соберём неизвестные слагаемые в левой части уравнения, а известные - в правой и приведём подобные слагаемые. Получим уравнение 7х = 21, отсюда х = 3.
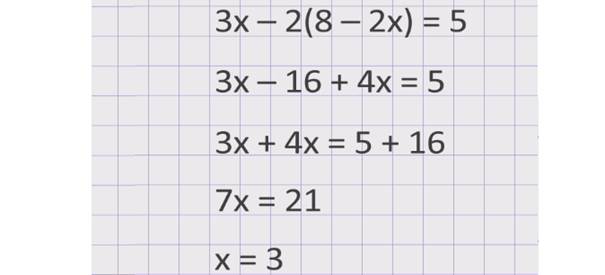
Теперь, используя найденное значение х, можно найти:

Ответ: пара чисел (3; 2).
Таким образом, на этом уроке мы научились решать системы уравнений с двумя неизвестными аналитическим, точным способом, не прибегая к сомнительному графическому.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!