В этом уроке рассмотрим такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата.

Давайте начертим квадрат со стороной 1 см.

Площадь одного такого квадратика называют квадратным сантиметром.

Пишут так:

один сантиметр в квадрате (1 см2).

Соответственно можем сделать вывод, что если какую – либо фигуру можно разбить на несколько таких квадратов, например, р квадратов, то ее площадь равна р см2.

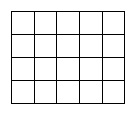
Перед вами рисунок, на котором изображен прямоугольник.

Он состоит из 4 полос, каждая из которых разбита на 5 квадратов со стороной 1 см.

Т.е. весь прямоугольник состоит из 20 квадратов (мы 4 умножили на 5, получили 20).

Значит площадь такого прямоугольника равна 20 см2.

Таким образом, получили правило:

Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.

Это правило можно записать в виде формулы.

Для этого обозначим площадь прямоугольника буквой S, кстати площади всех фигур принято обозначать этой буквой, длину прямоугольника буквой a, ширину – буквой b.

Получаем формулу площади прямоугольника: S равно а умножить на b(S = аb).

Теперь давайте рассмотрим следующую фигуру – квадрат, это тоже прямоугольник, но у него все стороны равны. Так как квадрат является прямоугольником, то воспользуемся формулой площади прямоугольника (S = аb). Но в случае квадрата b будет равно а, т.е. площадь равна а умножить на а, или принято записывать а в квадрате, значит: (S = а2). Получили еще одну формулу – формулу площади квадрата. 

Начертим квадрат со стороной 5 см и найдем его площадь.

Площадь квадрата со стороной 5 см равна 5 в квадрате, т.е. 25 см2.

Давайте рассмотрим две фигуры:

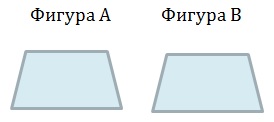
Как узнать равны ли эти фигуры?

Это легко проверить, если выполнить наложение, т.е. одну фигуру наложить на другую. Если они полностью совместятся или совпадут, то они равные.

Таким образом, сформулируем правило:

Две фигуры называются равными, если они совпадут при наложении.

А как вы думаете, равны ли их площади и периметры? Конечно, да! Площади равных фигур равны. Периметры равных фигур равны. Но не всегда выполняется наоборот.

Например, прямоугольник со сторонами 16 и 4 см имеет площадь 64 см2 и квадрат со стороной 8 см тоже имеет площадь 64 см2, но эти фигуры не равны между собой.

Давайте построим прямоугольник ABCD со сторонами 7 см и 4 см.

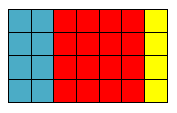
Разделим его на несколько частей.

Первая часть состоит из 8 см2, вторая часть – из 16 см2, третья часть – из 4 см2.

Если сложить все эти части, получим 8 + 16 + 4 = 28. Т.е. сумма площадей всех частей также равна 28 см2.

Итак, можно сделать вывод, что площадь всей фигуры равна сумме площадей ее частей.

Таким образом, на этом уроке мы рассмотрели такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата.