В этом уроке Вы познакомитесь с таким понятием как объем, узнаете о единицах измерения объёма, а также научитесь находить объем прямоугольного параллелепипеда.

Объем – это количественная характеристика пространства, занимаемого телом. Объем тела или фигуры определяется его формой и размерами.

Единицами измерения объема являются:

кубический миллиметр,

кубический сантиметр,

кубический дециметр,

кубический метр,

кубический километр.

Кубический сантиметр – это объем куба с ребром 1 см, кубический метр – это объем куба с ребром 1 м, кубический дециметр – это объем куба с ребром 1 дм. Между прочим, кубический дециметр также называют литром. Т.е. 1 литр равен одному кубическому дециметру.

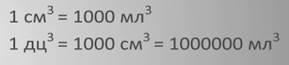
Единицы измерения объема связаны друг с другом.

Например,

1 кубический сантиметр = 1000 кубическим миллиметрам,

а 1 кубический дециметр – это 1000 кубических сантиметров или 1 000 000 кубических миллиметров.

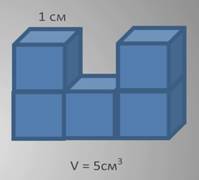
Рассмотрим фигуру, состоящую из 5 кубиков с ребром 1 см.

Так как объем каждого кубика составляет 1 кубический сантиметр, значит, объем всей фигуры равен 5 кубическим сантиметрам.

Т.е. можно сделать вывод, что объем всей фигуры равен сумме объемов ее частей.

Давайте выведем правило для вычисления объема прямоугольного параллелепипеда.

Пусть прямоугольный параллелепипед имеет длину 5 см, ширину 3 см и высоту 2 см.

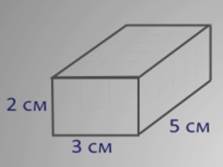
Разобьём его на два слоя толщиной 1 см каждый.

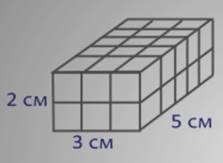
Т.е. первый слой состоит из 15 кубиков, так как в длину 5 кубиков и в ширину 3 кубика, а 5 умножить на 3, будет 15. Второй слой такой же.

Значит, чтобы найти объем всего параллелепипеда надо 15 умножить на 2.

Т.е. перемножили 5 и 3 – длину и ширину, а затем помножили на 2, т.е. на высоту.

Таким образом, получили правило:

Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.

В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. Volume — «объём» или «наполнение».

Формула объема прямоугольного параллелепипеда имеет вид:

V = авс, где V – это объем, а, в, и с – измерения (т.е. длина, ширина, высота). 

Давайте решим задачу, например, найти объем прямоугольного параллелепипеда, длина которого равна 10 см, ширина 4 см, высота 3 см.

Решение: чтобы найти объем прямоугольного параллелепипеда, нужно перемножить длину, ширину и высоту, т.е. 10 умножить на 4 и умножить на 3, получаем 120.

Ответ: объем равен 120 кубическим сантиметрам.

Таким образом, на этом уроке Вы познакомились с таким понятием как объем, узнали о единицах измерения объёма – кубические миллиметры, кубические сантиметры, кубические метры и так далее. А также получили правило для нахождения объема прямоугольного параллелепипеда: чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.