В этом уроке научимся делить сумму и разность на число.

Рассмотрим и решим следующую задачу.

В вазе лежало 15 яблок и 10 мандаринов. Эти фрукты раздали 5 детям поровну каждому. Сколько всего фруктов получил каждый ребенок?

Данную задачу можно решить двумя способами.

1 способ.

1) Найдем сначала, сколько всего было фруктов, и общее число фруктов разделим на количество детей.

2) Затем найдем значение этого выражения.

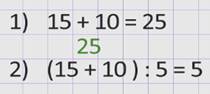
2 способ.

1) Найдем сначала, сколько яблок получил каждый ребенок.

2) Потом сколько мандаринов получил каждый ребенок.

3) Сложим частные, чтобы узнать сколько всего фруктов у каждого ребенка и найдем значение полученного выражения.

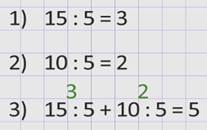
Значения обоих выражений одинаковые, значит, они равны.

Запишем равенство:

Частное суммы 15 и 10 и числа 5 равно сумме частных 15 и 5 и 10 и 5.

Рассмотрим выражения.

В первом выражении сумму делим на число.

Во втором выражении каждое слагаемое суммы делим на число, а результаты складываем.

Итак, правило деления суммы на число:

Если каждое слагаемое можно разделить на данное число, то, выполнив это деление и сложив полученные значения частных, мы найдем результат деления данной суммы на это число.

Перейдем к делению разности на число.

Рассмотрим выражения:

и

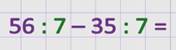
В первом выражении нужно разность разделить на число.

Найдем его значение:

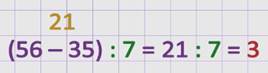
Обратите внимание на второе выражение, в нем разность двух частных.

Делимое первого частного является уменьшаемым в первом выражении, делимое второго частного является вычитаемым первого выражения.

Делитель в каждом частном является числом, на которое делится разность первого выражения.

Найдем значение второго выражения:

Значение обоих выражений одно и то же число, поэтому данные выражения равны.

Запишем равенство.

Частное разности 56 и 35 и числа 7 равно разности частных 56 и 7 и 35 и 7.

Выведем правило:

Если уменьшаемое и вычитаемое можно разделить на данное число, то, выполнив это деление и вычтя из первого полученного значения частного второе, мы найдем результат деления данной разности на это число.

Заметим, что в каждом случае при делении суммы на число или при делении разности на число слагаемые или уменьшаемое и вычитаемое должны делиться на данное число, чтобы правила можно было использовать.

Правила деления суммы на число и разности на число используют для удобства вычислений подобных выражений.

Например, сумму 56 и 72 разделить на 8

(56+72) : 8

удобнее сначала 56 : 8 = 7

потом 72 : 8 = 9

и наконец, сложить значения частных

7 + 9 = 16

Разность 140 и 35 разделить на 7

(140 – 35) : 7

удобнее 140 : 7 = 20

потом 35 : 7 = 5

20 – 5 = 15

Также данные правила используются при делении многозначного числа на однозначное.

55 : 5

Представим 55 суммой разрядных слагаемых 50 и 5.

Разделим сначала 50 на 5, получится 10.

Потом разделим 5 на 5, получится 1.

Затем сложим результаты 10 + 1 = 11.

Можно представлять делимое суммой удобных слагаемых.

Например, 96 : 8

Представим число 96 суммой удобных слагаемых, которые делятся на 8.

Это 80 и 16.

80 : 8 = 10, 16 : 8 = 2

Сложим значения частных 10 + 2 = 12.

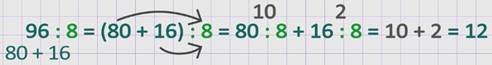
Чтобы найти значение частного 114 : 6, используем правило деления разности на число.

Для этого число 114 представим разностью чисел, которые делятся на 6.

Это 120 и 6.

120 : 6 = 20

6 : 6 = 1

20 – 1 = 19

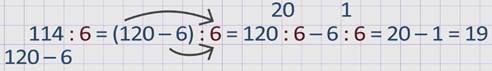
Итак, в этом уроке Вы познакомились с правилами деления суммы и деления разности на число и научились их применять.