На этом занятии мы с вами узнаем, что подразумевается под понятием «арифметический корень натуральной степени», а также рассмотрим свойства арифметических корней.
Решим уравнение: x4 =16.
Его можно представить в виде x4–16=0 или (x2–4)(x2+4)=0.
Это уравнение равносильно совокупности уравнений: x2–4=0, x2+4=0.
Т.к. x2+4=0 не имеет решения на множестве действительных чисел, то остается второе уравнение, решаем его: x2–4=0, x2=4, отсюда х1 = 2, х2 = -2.
Наше уравнение имеет два действительных корня, которые называются корнями четвертой степени из числа 16, а положительный корень (число 2) арифметическим корнем .
Арифметическим корнем натуральной степени n ≥ 2из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
подкоренным выражением.
Эти два условия позволяют осуществлять доказательство того, что заданное число равняется или не равняется заданному арифметическому корню натуральной степени.
Если степень арифметического корня n=2, то его называют квадратным корнем 
Действие, при котором находится корень n-ой степени, называется извлечением корня n-ой степени.
Оно является обратным действию возведения в n-ую степень.
Представим его в виде x3+ 64=0или (x+4)(x2-4x +16)=0.
(x+4)((x –2)2+12)=0
Поскольку (x-2)2 + 12 ≠ 0, то решаем уравнение x + 4 = 0, откуда x = -4.
Т.к. - 4 < 0, то число - 4, являясь корнем числа - 64, не является арифметическим корнем. .
Его называют корнем нечетной степени из отрицательного числа.
Корень нечетной степени из отрицательного числа а связан с арифметическим корнем из
Арифметический корень n-ой степени обладает несколькими свойствами:
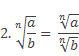
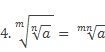
при условии, что a≥0, b>0, а n, m, k - натуральные числа, причем n≥2, m≥2.
Следует отметить, что для первого свойства допустимо значение b=0, а для третьего свойства число m может быть любым целым числом, если а>0.
Рассмотрим свойства на примерах:
2.
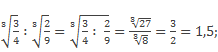
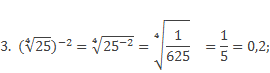
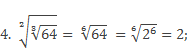
Итак, на этом уроке Вы познакомились с арифметическим корнем натуральной степени, с корнем нечетной степени из отрицательного числа, рассмотрели свойства арифметического корня, а также примеры на практическое использование этих свойств.
Подпишись и будь
в курсе новых событий и новостей!
