Изучим способы описания механического движения, рассмотрим задачи на расчет пути и времени движения разных тел.

Известно, что скорость при равномерном движении равна отношению пройденного пути ко времени движения:

Зная скорость, можно определить пройденный путь или время движения.

Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время, в течение которого этот путь пройден:

Чтобы определить время при равномерном движении, нужно пройденный путь разделить на скорость тела:

При неравномерном движении для расчета пути и времени используется средняя скорость на всем пути движения:

Задача № 1. Автомобиль за первые 10 мин проехал 900 м. Какой путь он пройдет за 0,5 ч, двигаясь с той же скоростью?

Запишем условие задачи, используя буквенные обозначения.

Весь пройденный путь состоит из двух участков, поэтому величины обозначим с индексами 1 и 2: время, в течение которого пройдена первая часть пути, t1 = 10 мин, в системе СИ 600 с, путь s1 = 900 м. Время, затраченное на вторую часть пути, t2 = 0,5 ч = 30 мин = 30*60 с = 1800 с. Известно, что скорость на всем пути одинакова: Найти путь s2.

Механическое движение можно описать не только аналитически при помощи формул, но и графически.

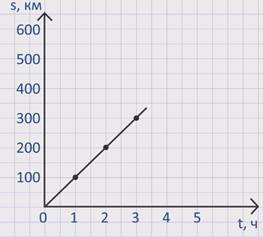
На графике зависимости пути от времени по вертикали откладывается пройденный путь, по горизонтали –время движения тела, причем единичные отрезки по оси пути и по оси времени можно выбрать разные. На графике отмечаем точки с координатами, соответствующими времени и пути, пройденному за это время. Например, поезд за 1 час проехал 100 км, отметим точку с координатами (1, 100), за 2 часа проехал путь 200 км – точка имеет координаты (2, 200), за 3 часа проехал 300 км – точка с координатами (3, 300). Через эти точки проводим прямую, которая представляет собой график пути при равномерном движении.

Задача № 2. На рисунке 2 представлены графики зависимости пути от времени для двух тел, движущихся равномерно. Определите скорости этих тел.

Анализируя графики и полученные значения скорости движения тел, можем сделать вывод: если угол наклона графика к оси времени больше, то скорость движения тела больше, угол наклона меньше – скорость меньше.

Задача №3. На рисунке 3 показан график зависимости скорости равномерного движения от времени (вертикальная ось – ось скорости , горизонтальная ось – ось времени t). Рассчитайте путь, который проедет тело за 2 часа.

Задача № 4. Трамвай прошел первые 100 м со средней скоростью 5 м/с, а следующие 600 м со средней скоростью 10 м/с. Определите среднюю скорость трамвая на всем пути.

Условие задачи: Известны путь и скорость трамвая на первом участке пути:

Найти среднюю скорость на всем пути.

Итак, важнейшей характеристикой механического движения является скорость. В формуле скорости выражена связь основных величин – скорости, пути и времени. Движение может быть описано при помощи графиков пути и скорости в зависимости от времени, что является более наглядным представлением движения тел.

Скорость при равномерном движении равна отношению пройденного пути ко времени движения:

Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время, в течение которого этот путь пройден: 

Чтобы определить время при равномерном движении, нужно пройденный путь разделить на скорость тела:

При неравномерном движении для расчета пути и времени используется средняя скорость на всем пути движения:

По графику зависимости пути равномерного движения от времени можно определитьпройденный путь за какой-либо промежуток времени и вычислить скорость движения. По графику скорости равномерного движения в зависимости от времени можно определить скорость тела и вычислить путь, пройденный телом за любой промежуток времени.