В этом уроке докажем две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и рассмотрим задачу на их применение.

Теорема 1.

Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.

Дано: неразвернутые углы АОВ и МNК, и ОА||NМ, ОВ||NК.

Доказать: либо углы АОВ и МNК равны, либо сумма углов АОВ и МNК равна 180º.

Рассмотрим случаи расположения углов АОВ и МNК (см. рисунок).

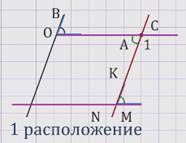
Доказательство для первого расположения углов.

Прямая NК пересекает прямую ОА в некоторой точке С.

Параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.

Параллельные прямые ОА и NМ пересечены секущей NС, поэтому угол 1 равен углу МNК – как накрест лежащие углы при параллельных прямых ОА и NМ и секущей NС.

Из двух равенств получаем, что ∠АОВ = ∠МNК.

При втором расположении углов:

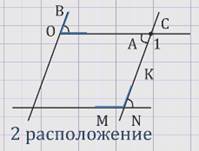
параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.

Параллельные прямые ОА и NМ пересечены секущей NС, поэтому сумма угла 1 и угла МNК = 180º, как сумма односторонних углов при параллельных прямых ОА и NМ и секущей NС.

Из двух равенств получаем, что ∠ АОВ + ∠МNК = 180º.

Теорема доказана.

Рассмотрим следующее утверждение.

Теорема 2.

Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.

Дано:

неразвернутые углы АОВ и A1O1B1, луч ОА перпендикулярен лучу O1A1, луч ОВ перпендикулярен лучу O1B1.

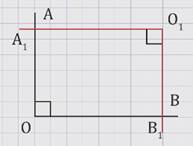
Доказать:

либо углы АОВ и A1O1B1 равны, либо сумма углов АОВ и A1O1B1 равна 180º.

Доказательство:

здесь необходимо рассмотреть несколько случаев.

Если угол АОВ прямой, то и угол A1O1B1 тоже прямой, поэтому эти углы равны и в сумме составляют 180º.

Остаются варианты, когда угол АОВ меньше 90º и когда угол АОВ больше 90º.

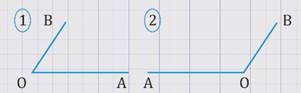
Рассмотрим подробнее первый случай.

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными, а точки В и С лежали по разные стороны от прямой ОА.

Теперь проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными, а точки С и D лежали по одну сторону от прямой ОА.

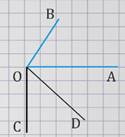
Так как угол АОВ равен 90º минус угол АОD и угол СОD равен 90º минус угол АОD по построению, то из двух этих равенств следует, что угол АОВ равен углу СОD.

Используя утверждение о том, что две прямые, перпендикулярные одной и той же прямой, параллельны, можно прийти к выводу, что стороны угла СОD соответственно параллельны сторонам угла A1O1B1, поэтому либо ∠СОD = ∠A1O1B1, либо сумма углов ∠СОD и ∠ A1O1B1= 180º.

Следовательно, либо ∠АОВ = ∠A1O1B1, либо сумма углов ∠АОВ и ∠A1O1B1= 180º.

Второй случай, когда угол АОВ больше 90º, докажите самостоятельно.

Задача.

Прямые, содержащие высоты АA1 и ВB1 треугольника АВС, пересекаются в точке Н, угол В – тупой, угол С = 20º.

Найти угол АНВ.

Решение:

Так как треугольник тупоугольный, угол В тупой, то высоты АA1 и ВB1 треугольника АВС пересекутся в точке Н за пределами треугольника (см. рисунок).

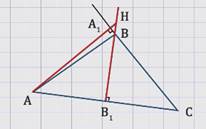
Рассмотрим углы АНB1 и АСA1.

Стороны угла АНB1 соответственно перпендикулярны сторонам угла АСA1, а по ранее доказанной теореме такие углы равны.

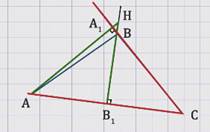
Значит, угол АНВ = 20º.

Итак, в этом уроке мы доказали две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и решили задачу по теме урока.