Если взять несколько прямых по-разному расположенных, то можно заметить, что они либо имеют одну общую точку, т.е. пересекаются, либо не имеют ни одной общей точки, т.е. не пересекаются.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Параллельность прямых обозначают b||c и говорят: «прямая b параллельна прямой c».
Отрезки, лежащие на параллельных прямых, называют параллельными отрезками.
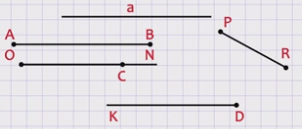
Аналогично определяется параллельность прямой и отрезка, отрезка и луча, луча и прямой, двух лучей. На рисунке отрезки АВ и ОС параллельны (АВ||ОС), а отрезки АВ и РR не параллельны. Параллельны прямая а и отрезок АВ, отрезок ОС и луч DК, лучи ОN и DК.
Параллельные отрезки часто встречаются в жизни. Например, рельсы железнодорожного пути на отдельных участках дороги параллельны друг другу, линии в разлинованной тетради, косяки дверей.
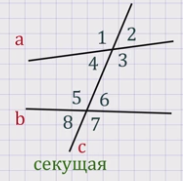
Давайте рассмотрим углы, которые образуются при пересечении двух прямых третьей.
На рисунке прямая c пересекает прямые а и b. При этом образовалось восемь углов.
Прямую с называют секущей, а образованные при этом углы попарно имеют специальные названия:
1 и 5, 4 и 8, 2 и 6, 3 и 7 – это соответственные углы;
4 и 6, 3 и 5 –это накрест лежащие углы;
4 и 5, 3 и 6 – это односторонние углы.
На рисунке углы в каждой из указанных пар не равны друг другу, и прямые а и b не параллельны. Но существуют три признака параллельности двух прямых, связанных с этими парами углов. Рассмотрим их.
Теорема 1: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Дано: прямые а и b и секущая АВ, накрест лежащие углы равны, т.е. угол 1 = углу 2.
Доказать: прямые а и b параллельны.
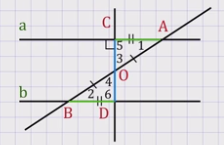
Доказательство: пусть накрест лежащие углы 1 и 2 равны по 90°, тогда прямые а и b перпендикулярны к прямой АВ, а значит, параллельны.
Теперь рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведем перпендикуляр ОС к прямой а. На прямой b от точки В отложим отрезок ВD, равный отрезку АС. Соединим точки О и D. Рассмотрим треугольники ОСА и ОDВ. Они равны по двум сторонам АО равен ВО, АС равен ВD и углу между ними, угол 1 равен углу 2. В равных треугольниках все соответствующие углы равны: угол 3 равен углу 4, угол 5 равен углу 6. Так как угол 3 равен углу 4, то точка D лежит на продолжении луча ОС, то есть точки С, О и D лежат на одной прямой. А так как угол 5 – прямой и равен углу 6, то угол 6 тоже прямой. Итак, прямые а и b перпендикулярны к прямой СD, поэтому прямые а и b параллельны. Теорема доказана.
Теорема 2: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
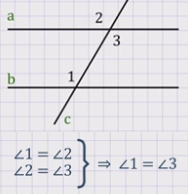
Дано: прямые а и b и секущая с, соответственные углы равны, т.е. угол 1 = углу 2.
Доказать: прямые а и b параллельны.
Доказательство: угол 2 равен углу 3, так как они вертикальные. Угол 1 равен углу 2 – это дано. Из этих двух равенств следует, что угол 1 равен углу 3. А углы 1 и 3 – накрест лежащие, значит, по уже доказанной нами теореме прямые а и b параллельны.
Что и требовалось доказать.
Теорема 3: Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.
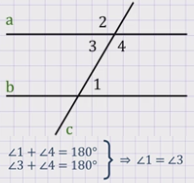
Дано: прямые а и b и секущая с, сумма односторонних углов равна 180º, например, угол 1 + угол 4 = 180º.
Доказать: прямые а и b параллельны.
Доказательство: сумма углов 1 и 4 равна 180º. Так как углы 3 и 4 смежные, то сумма углов 3 и 4 тоже равна 180º. Из этих двух равенств следует, что углы накрест лежащие 1 и 3 равны, значит, прямые а и b параллельны.
Теорема доказана.

Опираясь на признаки параллельности прямых, можно строить параллельные прямые с помощью линейки и чертежного угольника. Сдвигая угольник, приложенный стороной прямого угла к неподвижной линейке, проводим вдоль стороны, лежащей против прямого угла, прямые. При таком построении прямые всегда параллельны, так как соответственные углы всегда равны.

Построение параллельных прямых можно выполнить с помощью других инструментов, например, рейсшины(линейки с перекладиной на одном конце) или при помощималки(двух планок, скрепленных шарниром).
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!