Рассмотрим такую реальную ситуацию:

Мастер и ученик вместе изготовили на заказ 400 деталей. Причём мастер работал 3 дня, а ученик 2 дня. Сколько деталей изготовил каждый?

Составим алгебраическую модель данной ситуации. Пусть мастер изготавливает за 1 деньхдеталей. А ученик у деталей. Тогда мастер за 3 дня изготовит 3х деталей, а ученик изготовит за 2 дня 2у деталей. Вместе они изготовят 3х + 2удеталей. Так как по условию всего изготовлено 400 деталей, то получим уравнение:

3х + 2у = 400

Полученное уравнение называют линейным уравнением с двумя переменными. Здесь нам надо найти пару чисел х и у, при которых уравнение примет вид верного числового равенства. Заметим, что если х= 90, у = 65, то получим равенство:

3 ∙ 90 + 65 ∙ 2 = 400

270 + 130 = 400

400 = 400

Так как получено верное числовое равенство, то пара чисел 90 и 65 будет являться решением этого уравнения. Но найденное решение не единственно. Если х = 96 и у = 56, то получаем равенство:

96 ∙ 3 + 56 ∙ 2 = 400

288 + 112 = 400

400 = 400

Это тоже верное числовое равенство, а, значит, пара чисел 96 и 56 так же является решением этого уравнения. А вот пара чисел х= 73и у= 23 не будет являться решением этого уравнения. В самом деле, 3 ∙ 73 + 2 ∙ 23 = 400 даст нам неверное числовое равенство 265 = 400.Необходимо отметить, что если рассматривать уравнение применительно к данной реальной ситуации, то будут существовать пары чисел, которые, являясь решением данного уравнения, не будут являться решением задачи. Например, пара чисел:

х = 200 и y = –100

является решением уравнения, но ученик не может сделать -100 деталей, а поэтому такая пара чисел ответом на вопрос задачи быть не может. Таким образом, в каждой конкретной реальной ситуации необходимо разумно подходить к отбору корней уравнения.

Подведём первые итоги:

Уравнение вида ах + bу + с = 0, где а, b, с – любые числа, называют линейным уравнением с двумя переменными.

Решением линейного уравнения с двумя переменными называют пару чисел соответствующих х и у, при которых уравнение обращается в верное числовое равенство.

Сама запись пары (х;у) наталкивает нас на мысль о возможности изображения её в виде точки с координатами хи у на плоскости. А значит, мы можем получить геометрическую модель конкретной ситуации. Например, рассмотрим уравнение:

2х + у – 4 = 0

Подберём несколько пар чисел, которые будут являться решениями этого уравнения и построим точки с найденными координатами. Пусть это будут точки:

А(0; 4), В(2; 0), С(1; 2), D(–2; 8), Е(– 1; 6).

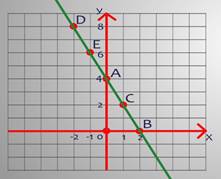
Заметим, что все точки лежат на одной прямой. Такую прямую называют графиком линейного уравнения с двумя переменными. Она является графической (или геометрической) моделью данного уравнения. 

Если пара чисел (х;у) является решением уравнения

ах + ву + с = 0, то точка М(х;у) принадлежит графику уравнения. Можно сказать и наоборот: если точка М(х;у) принадлежат графику уравнения ах + ву + с = 0, то пара чисел (х;у) является решением этого уравнения.

Из курса геометрии мы знаем:

Для построения прямой необходимо 2 точки, поэтому для построения графика линейного уравнения с двумя переменными достаточно знать всего 2 пары решений. Но угадывание корней процедура далеко не всегда удобная, не рациональная. Можно действовать и по другому правилу. Поскольку абсцисса точки (переменная х) это независимая переменная, то можно придать ей любое удобное значение. Подставив это число в уравнение, мы найдём значение переменной у.

Например, пусть дано уравнение:

х – у + 1 = 0

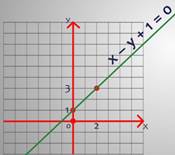
Пусть х = 0, тогда получим 0 – у + 1 = 0 или у = 1. Значит, если х = 0, то у = 1. Пара чисел (0;1) – решение этого уравнения. Зададим для переменной х ещё одно значение х = 2. Тогда получим 2 – у + 1 = 0 или у = 3. Пара чисел (2;3) также является решением этого уравнения. По двум найденным точкам уже можно построить график уравнения х – у + 1 =0.

Можно поступить и так: сначала придать некоторое конкретное значение переменной у, а уж потом вычислить значение х.

Найдите два натуральных числа, сумма которых 11, а разность 1.

Для решения этой задачи сначала составим математическую модель (а именно алгебраическую). Пусть первое число х, а второе – у. Тогда сумма чисел х + у = 11 и разность чисел х – у = 1. Так как в обоих уравнениях речь идёт об одних и тех же числах, то данные условия должны выполниться одновременно. Обычно в таких случаях используют специальную запись. Уравнения записывают одно под другим и объединяют фигурной скобкой.

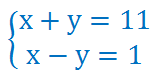
Такую запись называют системой уравнений.

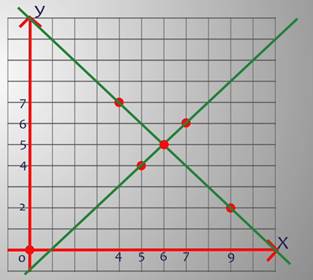
Теперь построим множества решений каждого уравнения, т.е. графики каждого из уравнений. Возьмём первое уравнение:

х + у = 11

Если х =4, то у = 7. Если х = 9, то у = 2.

Через точки (4;7) и (9;2) проведём прямую.

Возьмём второе уравнение х – у = 1. Если х = 5, то у = 4. Если х = 7, то у = 6. Через точки (5;4) и (7;6) так же проведём прямую. Получили геометрическую модель задачи. Интересующая нас пара чисел (х;у) должна являться решением обоих уравнений. На рисунке мы видим единственную точку, которая лежит на обеих прямых, это – точка пересечения прямых.

Её координаты (6;5). Поэтому решением задачи будет: первое искомое число 6, второе 5.