Очень часто в жизни мы сталкиваемся с ситуацией, когда рассматриваются 2 связанные друг с другом величины. Например, поездка в поезде. Выбрать станцию назначения мы можем, а вот стоимость поездки именно до этой станции от нас не зависит. Или покупки в магазине. Выбрать товар мы можем, а вот стоимость выбранной покупки опять-таки нет. В рассмотренных примерах одна из величин является свободной для выбора, а вот другую мы свободно выбрать не можем. Причём вторая величина определяется однозначно и зависит от первой. На самом деле мы имеем дело с так называемыми функциональными зависимостями.

Функция – это зависимость, при которой каждому значению независимой переменной соответствует не более одного значения зависимой переменной.

Давайте рассмотрим это понятие применительно к линейным уравнениям с двумя переменными.

К уравнениям вида ах + bу + с = 0.Такие уравнения имеют бесконечно много решений, которые можно изобразить на координатной плоскости в виде прямой. Для построения прямой необходимы 2 точки. Чтобы их найти одной из переменных придают конкретные значения и вычисляют соответствующие значения другой. При этом приходится дважды решать одно и то же уравнение. Но математики решили упростить себе задачу. Они решили не выполнять одну и ту же работу дважды, а сразу выразить одну из переменных через другую. Договорились, что будем выражать переменную у через переменную х. Сначала оставим слагаемое с переменной у слева, а остальные слагаемые перенесём вправо. Получим:

bу = -ах – с

Теперь разделим обе части равенства на b. Получим:

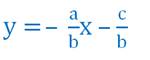
Теперь нам достаточно взять два различных значения х и, подставив их в полученное равенство, найти значения у. Здесь переменная х будет называться независимой переменной или аргументом, а переменная у – зависимой переменной или значением функции.

Необходимо построить график линейного уравнения 4х + 2у – 8 = 0.

Выразим переменную у через х. Получим 2у = - 4х + 8 или у = - 2х + 4. Придадим переменной х конкретные значения.

Если х = 0, то у = - 2 ∙ 0 + 4 = 4. Первая точка (0; 4)

Если х = 2, то у = - 2 ∙ 2 + 4 = 0. Вторая точка (2; 0).

Результаты удобно заносить в таблицу:

Через полученные 2 точки можно провести прямую, которая и будет искомым графиком.

Таким образом, линейное уравнение с двумя неизвестными приобрело вид: у = kх + m. Фактически это правило, по которому можно найти значение у, зная значение х. Такую запись называют линейной функцией.

Так как линейная функция это частный вид линейного уравнения, то её графиком является прямая.

На самом деле многие реальные ситуации описываются моделями, представляющими собой линейные функции. Например:

На овощебазе было 1200 тонн картофеля. Ежедневно в магазины развозили по 30 тонн. Сколько картофеля останется на складе через 2дня, 3 дня, 6 дней?

Пусть у – искомый остаток, х – количество дней. Тогда ежедневно со склада будут вывозить 30х тонн и остаток будет у = 1200 – 30х.

При х = 2 имеем у = 1200 – 30 ∙ 2 = 1140

При х = 3 имеем у = 1200 – 30 ∙ 3 = 1110

При х = 6 имеем у = 1200 – 30 ∙ 6 = 1020

Ответ задачи: на складе картофеля останется через 2 дня 1140 тонн, через 3 дня 1110 тонн, через 6 ней 1020 тонн.

Важно отметить, что в каждой конкретной ситуации необходимо учитывать возможные ограничения на переменные. В нашем примере мы понимаем, что переменная у может принимать только неотрицательные значения или у ≥ 0, а переменная х – принимать значения не менее 0 и не более 40, то есть 0 ≤ х ≤ 40