В этом уроке вы узнаете, как сравнивать десятичные дроби, а также рассмотрите изображение десятичных дробей на координатном луче.

Давайте вспомним, что десятичной дробью называют число, записанное в десятичной системе и имеющее разряды меньшие единицы, например, 26,4; 3,25; 0,145 и т. д.

Знаки, стоящие в десятичной дроби после запятой, называют десятичными знаками.

Десятичная дробь не изменится, если в конце дроби приписать или отбросить нули. Например:

12,3 = 12,30 = 12,300 и т.д., т.е. мы приписали нули в конце десятичной дроби.

Другой пример:

6, 300 = 6,3 здесь, наоборот, мы отбросили два нуля.

Как вы знаете, два числа могут быть равны между собой, или не равны. Целые числа вы уже умеете сравнивать, например, 247 больше 146.

А какая дробь больше 247,3 или 146,9?

На этот вопрос вы легко дадите ответ, конечно, 247,3! Потому что больше та дробь, у которой целая часть больше! Вот оно – первое правило.

Чтобы сравнить две десятичные дроби, нужно вначале сравнить их целые части.

Та десятичная дробь больше, у которой целая часть больше. И наоборот, та десятичная дробь меньше, у которой целая часть меньше.

А как же быть, если целые части у сравниваемых дробей одинаковые?

Например: 21,105 и 21,7?

Целые части равны, сравним дробные: для начала, уравняем число знаков после запятых, приписав к дроби 21,7 справа два нуля, получим 21,700.

Сравниваем: 105 тысячных меньше, чем 700 тысячных, значит 21,105 меньше 21,7. Оказывается, можно сравнить эти дроби поразрядно: первый разряд 1 меньше 7, значит 21,105 меньше 21,7.

Получили второе правило: при равенстве целых частей у десятичных дробей сравниваются дробные части. Если число символов после запятой у сравниваемых дробей не совпадает, тогда к дроби с меньшим количеством символов приписываем нули и сравниваем получившиеся числа дробных частей. Сравнение дробной части десятичной дроби производится по разрядам от меньшего к большему (т.е. сначала десятые, потом при необходимости сотые, тысячные и т.д.). Та десятичная дробь больше, у которой величина числа в разряде больше.

Рассмотрим пример:

необходимо сравнить дроби 0,367 и 0,354.

Так как целые части равны, то сравнить надо дробные части:

1 -й разряд: 3 = 3,

переходим к сравнению во втором разряде: 6 > 5.

Следовательно, 0,367 > 0,354.

Десятичные дроби, как и натуральные числа, можно записать в возрастающий (или убывающий) ряд. На числовой оси правее стоит та десятичная дробь, которая больше, а левее — та, которая меньше.

Например, если сравнить дроби 0,6 и 0,85, на числовой оси это выглядит так:

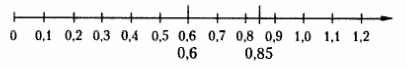
0,85 стоит правее на числовой оси: 0,85 > 0,6.

Таким образом, можно сформулировать еще одно правило: чем больше десятичная дробь, тем правее она расположена на координатном луче, и наоборот, чем меньше десятичная дробь, тем левее она расположена на координатном луче.