Давайте прибавим к натуральному числу единицу. Что получится? Например, 7 + 1 = 8 или 123 + 1 = 124. Получится следующее за ним число.

А теперь попробуем сложить числа 7 и 3. Это значит прибавить к числу 7 три раза единицу. Получим: 7 + 3 = 7 + 1 + 1 + 1 = 8 + 1 + 1 = 9 + 1 = 10. На практике пишут короче 7 + 3 = 10.

Числа, которые мы сложили, называют слагаемыми. А число, получившееся при их сложении, называют суммой. В нашем примере числа 7 и 3 – это слагаемые, а число 10 – сумма.

Сложение чисел можно проиллюстрировать на координатном луче. Например, 4 +3 = 7. Как вы видите, из точки с координатой 4 передвигаемся вправо на три деления и попадаем в точку с координатой 7.

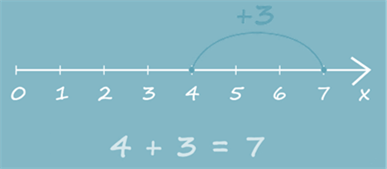
При сложении натуральных чисел можно использовать следующие свойства:

1.Переместительное свойство сложения: при перестановке слагаемых сумма не меняется. Например, 3 + 6 = 9 и 6 + 3 = 9.

С помощью букв это свойство можно записать таким образом: a + b = b + a.

2.Сочетательное свойство: чтобы к числу прибавить сумму двух чисел, можно к этому числу сначала прибавить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое. Например, 3 + (2 + 6) = 3 + 8 = 11, или же воспользуемся свойством и выполним сложение так: 3 + 2, будет 5 и прибавим 6, получится 11.

С помощью букв это свойство можно записать таким образом: a + (b + c) = (a + b) + c.

3.Свойство нуля: если к числу прибавить нуль, то получится само число. Например, 8 + 0 = 8. Кстати сказать, что и 0 + 8 = 8. Так как от перестановки слагаемых сумма не меняется и 8 + 0 = 0 + 8 = 8. Значит, если к нулю прибавить какое – нибудь число, то получится прибавленное число.

С помощью букв это свойство можно записать таким образом : a + 0 = 0 + a = а.

Очень часто эти свойства работают в паре.

Давайте рассмотрим несколько заданий с использованием вышеперечисленных свойств.

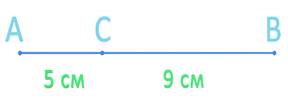
Задание № 1. Точка С лежит на отрезке АВ. Причем длина отрезка АС равна 5 см, длина отрезка СВ равна 9 см. Найдите длину отрезка АВ.

Решение: если точка С лежит на отрезке АВ, то длина всего отрезка АВ равна сумме длин его частей АС и СВ, то есть длина отрезка АВ = (АС + СВ) или (СВ + АС) = (5 + 9) или (9 + 5) = 14.

Ответ: длина отрезка АВ= 14 см.

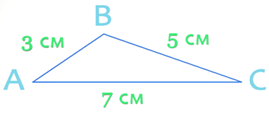
Задание № 2: найдите периметр треугольника АВС, если сторона АВ равна 3 см, сторона ВС равна 5 см, а сторона СА равна 7 см.

Решение: для начала вспомним, что такое периметр треугольника. Сумму длин всех сторон многоугольника называют периметром многоугольника. Значит, периметр треугольника АВС – это сумма трех его сторон АВ, ВС и СА. То есть, 3 + 5 + 7 = 15. Причем можно было сложить сначала 3 и 7, будет 10, 10+5 =15.

Ответ: периметр треугольника АВС равен 15 см.

Задание № 3. Вычислить: 89 + 0 + 54

89 + 0 + 54 = 89 + 0 = 89 + 54 = 143