В этом занятии научимся умножать многозначные числа на 10, 100, 1000, а также на «круглое» двузначное число.

Найдем значение произведения 1 десятка и четырех.

Произведение можно заменить суммой одинаковых слагаемых.

1 десяток – это число 10.

Произведение одного десятка и четырех равно сумме четырех одинаковых слагаемых, равных 10:

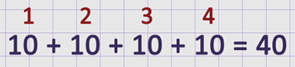
Таким образом:

Поменяем в произведении множители местами:

Вспомним переместительный закон умножения: при перестановке множителей значение произведения не меняется.

Значит:

Сравним записи чисел 4 и 40:

Сделаем вывод:

если к записи данного числа справа приписать цифру 0, то получится запись числа, которое в 10 раз больше данного.

А как умножить число на 100 или на 1000?

Рассуждаем аналогично:

Если 100 ∙ 3 = 300, то 3 ∙ 100 – равно тоже 300, так как при перестановке множителей значение произведения не меняется.

Сравним записи чисел 3 и 300:

Чтобы получить запись числа 300, нужно к записи числа 3 справа приписать два 0.

Значит, при умножении числа на 100, если к записи данного числа приписать два нуля, получится запись числа, которое и будет в 100 раз больше данного.

Найдем значение произведения:

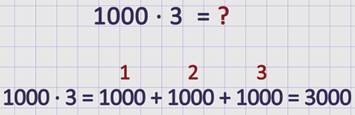
При умножении на 1000 к записи числа приписывается три нуля, получится запись числа, которое в 1000 раз больше данного.

Подведем итог.

·Если к записи данного числа справа приписать одну цифру 0, то получится запись числа, которое больше данного в 10 раз.

·Если к записи числа справа приписать две цифры 0, то получится запись числа, которое больше данного в 100 раз.

·Если к записи числа справа приписать три нуля, то получится запись числа, которое в 1000 раз больше данного.

Выполним еще одно задание.

Число 6 нужно сначала увеличить в 3 раза, а потом еще в 10 раз.

Увеличить в 3 раза – значит умножить на 3, увеличить в 10 раз – значит умножить на 10.

Получим выражение:

6 ∙ 3 ∙ 10 = ?

Вспомним сочетательный закон умножения: при умножении трех множителей можно перемножить любые два множителя, а потом результат умножить на третий множитель.

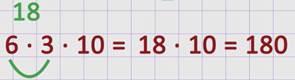
Используя сочетательный закон умножения, данное выражение мы можем записать как произведение 6 и произведения 3 и 10.

Значит, 6 ∙ 30 = 180.

Рассмотрим последнее выражение.

Сколько нулей во втором множителе?

Один.

В значении произведения тоже один нуль.

Как получилось в значении произведения 18?

Итак, чтобы число умножить на «круглое» двузначное число, нужно умножить его на количество десятков этого двузначного числа, а потом приписать к записи результата цифру ноль.

Например:

На этом уроке Вы научились умножать на 10, 100, 1000 и на «круглое» двузначное число.