Полная механическая энергия замкнутой системы тел, в которой действуют консервативные силы, сохраняется. Консервативными силами являются силы тяжести и силы упругости, их работа зависит от начального и конечного положения тела и не зависит, по какой траектории оно двигалось. Энергия не создается и не уничтожается, а только превращается из одного вида в другой: из кинетической в потенциальную и, наоборот, из потенциальной в кинетическую:

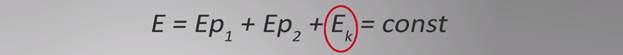
где Е – полная механическая энергия;

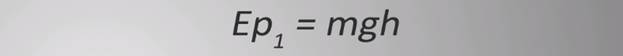
потенциальная энергия силы тяжести;

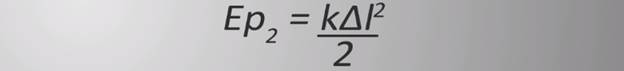
потенциальная энергия упругих сил;

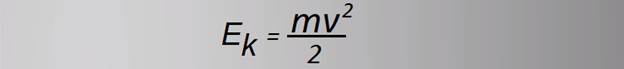
кинетическая энергия движущегося тела.

Механическая энергия в случае действия сил трения не сохраняется, кинетическая энергия уменьшается и при остановке тела полностью превращается во внутреннюю энергию хаотического движения молекул. Закон сохранения механической энергии может нарушаться, но закон сохранения полной энергии никогда не нарушается.

Решение: Запишем краткую запись. Нарисуем рисунок, отражающий условие задачи. По условию задачи молот падает на наковальню с заготовкой, поэтому сначала рассмотрим систему «молот – Земля». Пренебрегая силами сопротивления, будем считать эту систему замкнутой. Применим к системе «молот – Земля» закон сохранения механической энергии. Падение молота происходит под действием силы тяжести.

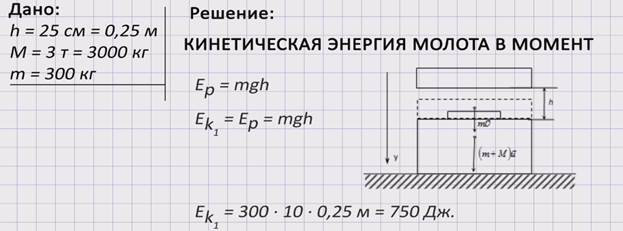
Рассмотрим систему «молот – заготовка – наковальня» в момент удара, когда происходит ковка заготовки. Система замкнутая, но неконсервативная, поэтому можно считать, что энергия, затраченная на деформацию заготовки Ед, равна разности значений механических энергий до и после удара. Во время удара изменяется только кинетическая энергия тел, так как незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда полезная энергия, затраченная на деформацию (ковку):

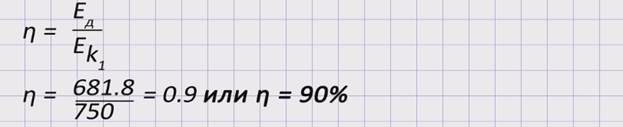
Ответ:Кинетическая энергия молота в момент перед ударом равна 750 Дж. Кинетическая энергия системы «молот – заготовка – наковальня» после удара – 68,2 Дж. Энергия, затраченная на ковку, составляет 681,8 Дж. Коэффициент полезного действия – 90%.

Рассмотрим замкнутую механическую систему «акробат – Земля» для момента, когда акробат свободно падает с высоты Н до сетки. В этой системе действуют только внутренние консервативные силы тяжести, поэтому для нее можно записать закон сохранения механической энергии.

Решая задачу с использованием закона сохранения механической энергии, необходимо выбрать систему тел, взаимодействие которых нужно рассмотреть. Определить, является ли эта система замкнутой, а внутренние силы консервативны, если эти условия выполняются, можно применять закон сохранения механической энергии.