В этом уроке разберем, что такое прямая и обратная пропорциональные зависимости, а также решим задачи на пропорциональные величины.
Две величины называют прямо пропорциональными, если при увеличении или уменьшении одной из них в несколько раз другая величина соответственно увеличивается или уменьшается во столько же раз.
Рассмотрим прямую пропорциональную зависимости на примере следующей задачи.
За два часа спортсмен пробежал 20 километров, сколько километров он пробежит за 6 часов, если его скорость не изменится?


Время спортсмена в пути увеличится в три раза, значит и количество километров, которое спортсмен пробежит, тоже увеличится в три раза, так как спортсмен бежит с постоянной скоростью. Во сколько раз увеличится время, во столько же раз увеличится расстояние. Зависимость между временем и расстоянием в данном случае прямо пропорциональна.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны. Значит, отношения значений времени 2 : 6 и значений расстояния 20 : х равны, следовательно, верна пропорция 2 : 6 = 20 : х. Теперь найдем неизвестный член пропорции: х = 6 · 20 : 2 = 60. Получаем, 60 километров пробежит спортсмен за 6 часов.
Две величины называют обратно пропорциональными, если пр. и увеличении или уменьшении одной из них в несколько раз другая величина соответственно уменьшается или увеличивается во столько же раз.
Рассмотрим и обратную пропорциональную зависимость на примере. Задача: Спортсмен пробежал расстояние со скоростью 5 км/ч за 6 часов, за сколько часов спортсмен пробежит это расстояние, если скорость его увеличится вдвое?
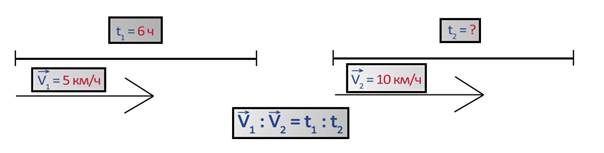
Если скорость увеличится вдвое, она будет равна 10 км/ч, и данное расстояние спортсмен пробежит быстрее вдвое, то есть затратит вдвое меньше времени на прохождение этого расстояния. Во сколько раз увеличится скорость, во столько раз уменьшится время его движения. Зависимость между скоростью движения и временем в пути в данном случае обратно пропорциональна.

Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины. Значит, отношение значений скорости 5 : 10 будет равно не отношению 6 : х, а обратному отношению соответствующих значений времених:6. Значит, верна пропорция 5 : 10 = х : 6, решаем:
х = 5 · 6 : 10 = 3. Получаем, что это же расстояние спортсмен пробежит за 3 часа, если его скорость увеличится вдвое.
Отметим, что не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, зависимость между возрастом человека и размером его обуви. При удвоении возраста человека размер его обуви не удваивается, поэтому величины возраст и размер обуви не являются пропорциональными. Не будут пропорциональными время и расстояние в нашей первой задаче, если скорость спортсмена не будет постоянной.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!