В этом уроке ответим на вопрос: как произвести оценку площади? А также научимся выполнять приближённое вычисление площади.

Давайте представим ситуацию.

Однажды ученики 4 класса побывали на кондитерской фабрике. Им показывали, как делают вафли. В конце экскурсии кондитер отломил каждому ученику от большой пластины по маленькому кусочку хрустящей вафли. Кусочки были неодинаковые. Петя и Вася стали спорить, чей кусок оказался больше.

Как же им помочь решить их спор? Можно конечно сравнить, наложив один кусок на другой. Но сравнение точным не получится, так как одну из фигур разместить внутри другой нельзя.

Какой же метод сравнения используют в случае, когда наложением сравнить нельзя? Конечно, нужно сделать измерения. Чтобы измерить площадь фигуры, нужно выбрать единицу измерения и определить, сколько раз она содержится в фигуре.

Единицы измерения площади – это квадратный миллиметр, квадратный сантиметр, квадратный метр, квадратный километр.

На рисунке мы видим, что вафли разделены на квадраты. Возьмём их за единицу измерения площади вафель. На рисунке также видно, что площадь вафель состоит из целых и нецелых квадратов.

Определим, между какими числами заключена площадь каждой вафли, т.е. сделаем оценку площади, найдём «нижнюю и верхнюю границы».

«Нижняя граница» – это меньшее число квадратов, значит, мы будем считать только целые квадраты внутри фигуры. Чтобы найти «верхнюю границу», нужно найти большее число квадратов. Значит, нужно найти количество всех целых и всех нецелых квадратов вместе.

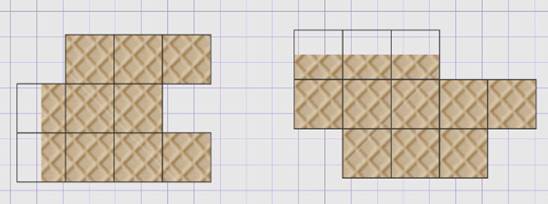
Итак, давайте сделаем оценку площади Петиной вафли.

Сосчитаем целые квадраты, их получилось 8. Это «нижняя граница» площади.

Сосчитаем все нецелые квадраты фигуры, их – 2, прибавим к целым, получилось 10. Это «верхняя граница» площади.

Значит, площадь Петиной вафли находится в границах от 8 до 10 квадратов. Это можно записать в виде двойного неравенства.

8 < S < 10

Теперь сделаем оценку площади Васиной вафли. Считаем все целые квадраты внутри фигуры, «нижняя граница» – 8. Считаем все нецелые квадраты фигуры и добавляем к целым, «верхняя граница» – 11. В результате мы получаем следующее неравенство, которое обозначает «нижнюю и верхнюю границы» площади Васиной вафли.

8 < S < 11

Таким образом, у нас получилось, что у мальчиков почти одинаковые по площади вафли.

Давайте обобщим, чтобы произвести оценку площади надо:

1. сосчитать число целых квадратов, расположенных внутри фигуры, то есть определить «нижнюю границу» площади.

2. сосчитать число нецелых квадратов фигуры и прибавить к ним количество всех целых квадратов, расположенных внутри фигуры, то есть определить «верхнюю границу» площади.

3. записать двойное неравенство, указав «верхнюю» и «нижнюю» границы площади.

А теперь вычислим площадь этих вафель.

Внутри вафель мы можем насчитать 8 целых квадратов. Остальные квадраты входят частично, поэтому число нецелых квадратов делим пополам. Итак, в Петиной вафле содержится 8 целых и 2 нецелых квадрата.

Значит, примерно 8 + 2 : 2 = 8 + 1 = 9 квадратов. (8 < 9 < 10).

В Васиной вафле содержится 8 целых и 3 нецелых квадрата.

Значит, 8 + 3 : 2. Так как число 3 нечётное и на 2 не разделится, его нужно увеличить на 1. Давайте 3 увеличим на 1, получим 8 + 4 : 2 = 8 + 2 = 10 квадратов. (8 < 10 < 11).

Так как мы можем посчитать количество квадратов только приблизительно. Мы не имеем право ставить знак «=» между найденным количеством квадратов и площадью. Поэтому для обозначения примерного результата используем знак приближенного равенства «≈».

S ≈ 9 ед2

S ≈ 10 ед2.

Читать следует так:

«Площадь приближенно равна 9 квадратным единицам».

«Площадь приближенно равна 10 квадратным единицам».

Таким образом, мы выполнили приближенное вычисление площади вафель Пети и Васи.

Вычислить приблизительную площадь вафель мы смогли благодаря тому, что фигуры были разделены на квадраты.

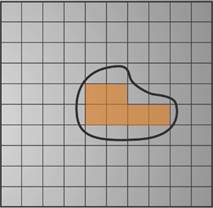
Что делать, если таких квадратов нет? Самим расчерчивать фигуры очень долго, поэтому люди придумали особое приспособление – палетку.

Палетка – прозрачная плёнка, разделённая на одинаковые квадраты.

Вычислим площадь фигуры при помощи палетки,

площадь каждой клетки которой равна 1 см2.

1. Наложим палетку на фигуру.

2. Сосчитаем число целых клеток внутри фигуры (а = 6).

3. Сосчитаем число клеток входящих в фигуру частично (b = 14).

4. Вычислим приближенное значение площади 6 + 14 : 2 = 6 + 7 = 13, S ≈13 см2.

Для вычисления приближенного значения площади используют формулу S ≈ а+b:2, где a - это число целых клеток, b – число нецелых клеток.

Для того чтобы произвести оценку площади, необходимо:

1. Сосчитать число целых квадратов, расположенных внутри фигуры, то есть определить «нижнюю границу» площади.

2. Сосчитать число нецелых квадратов фигуры и прибавить к ним количество всех целых квадратов, расположенных внутри фигуры, то есть определить «верхнюю границу» площади.

3. Записать двойное неравенство, указав «верхнюю» и «нижнюю» границы площади.

Для того чтобы вычислить площадь фигуры при помощи палетки, необходимо:

1. Наложить палетку на фигуру.

2. Сосчитать число а целых клеток внутри фигуры.

3. Сосчитать число b клеток, входящих в фигуру частично.

4. Вычислить приближенное значение площади: S ≈ а + b : 2 (если число b нечётно, то увеличить его на 1).