Предлагаю вспомнить главное условие сравнения площадей фигур с помощью мерок. Мерки должны быть одинаковыми по форме и по размеру. Например, для сравнения площадей данных фигур я выбрала мерку – квадрат.

Площадь первой фигуры 7 мерок, а площадь второй фигуры 6 мерок. Площадь первой фигуры больше площади второй фигуры и, наоборот, площадь второй фигуры меньше площади первой фигуры.

Попробуем изменить форму и размер мерки, разделив квадрат пополам. Получится треугольник. Можно узнать площадь первой фигуры, пересчитывая мерки, или, зная, что в квадрате два треугольника, по два взять семь раз. Получается 14 мерок. Площадь второй фигуры мы также определяем с помощью новой мерки – треугольника.
Более быстрый способ – умножение. По два треугольника возьмём 6 раз, получится 12 мерок. Сравнивая количество мерок после изменения их формы и размера, мы замечаем,
·во-первых, подтвердились наши выводы о соотношении площадей фигур: 14>12 (площадь впервой фигуры больше площади второй фигуры);
·во-вторых, изменение формы и размера мерок не нарушают процесс сравнения площадей, могут измениться только числовые значения, но результат от этого не изменится.
Рассмотрим внимательно данный прямоугольник.

Его площадь можно вычислить с помощью мерок-квадратов, мерок-прямоугольников и мерок-треугольников. Выбор мерок измерения площади будем делать по результату, представленному в таблице.
В левом столбце – числа, показывающие количество мерок в фигуре. В верхней строке таблицы нужно расположить различные мерки. Внимательно присмотримся к линиям на чертеже. Фигуру можно разделить на четыре равные части.
Её площадь соответствует четырём большим меркам-квадратам. Обозначим это в таблице.
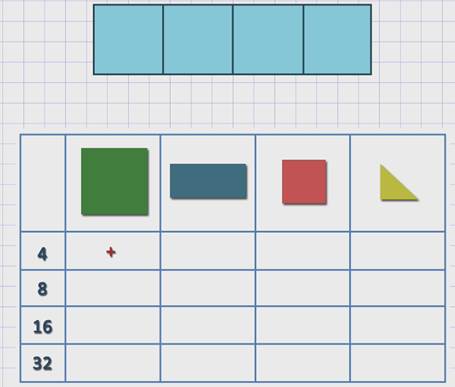
Далее рассуждаем: как из 4-х получить 8? Нужно по 2 взять 4 раза, значит, квадрат можно уменьшить вдвое. Получается прямоугольник. Проверим своё предположение пересчитыванием.
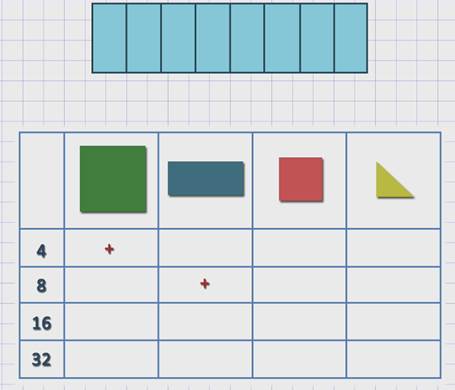
Верно, получилось 8 прямоугольников. Заносим данные в таблицу. Из таблицы умножения мы знаем, что значение произведения 16 можно получить двумя парами множителей: 8 и 2 или 4 и 4. Присмотримся к чертежу повнимательнее. Оказывается, каждый из 8 прямоугольников разделён на 2 одинаковых квадрата. Также можно рассмотреть 4 маленьких квадратика в каждом из 4-х больших квадратов. Таким образом, получается, что число 16 соответствует маленьким квадратикам-меркам. Отметим это в таблице.
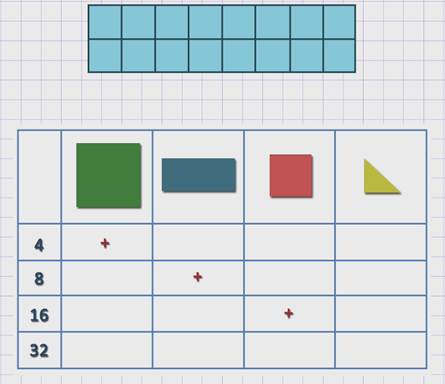
Остаётся самое большое число. Но, обратите внимание, из таблицы видно, что, чем больше число мерок, тем меньше размеры самой мерки и, наоборот, чем меньше число мерок, тем размеры мерки становятся больше.
Вывод напрашивается сам собой: наибольшее количество мерок предполагает самую маленькую по размеру мерку! Конечно это треугольник! Для проверки можно пересчитать все треугольники, а можно сделать вычисления. Треугольник – половина квадратика. Квадратиков 16, значит треугольников в два раза больше. По 16 взять 2 раза, это 16 плюс 16, получится 32. Мы доказали правильность своих предположений с помощью вычислений. Результаты заносим в таблицу.

Таким образом, осуществить выбор мерок для измерения площади фигуры возможно по результату – числовым данным. Для этого необходимо найти площадь данной фигуры с помощью различных мерок и сравнить с результатом.
Рассмотрим таблицу. Площадь данной фигуры будет иметь наибольшую величину в случае выбора мерки-треугольника (32 мерки), а наименьшую величину (4), если мерка – большой квадрат.
В процессе работы мы выявили зависимость между количеством мерок – результатом и размерами мерки. Чем больше число мерок, тем меньше размеры самой мерки и, наоборот, чем меньше число мерок, тем размеры мерки становятся больше. Важно отметить, что площадь одной и той же фигуры можно узнать, используя разные мерки. Это необходимо, например, при сравнении площадей фигур, когда мы должны использовать равные мерки. Сравним площади данных фигур.
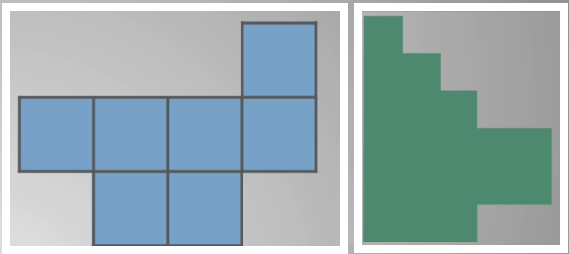
Синюю фигуру можно легко разделить на 7 равных частей-мерок, а зелёную с помощью таких же мерок разделить не получится. Поэтому выберем мерку меньшего размера, подходящую для зелёной фигуры. Это будет маленький квадрат.
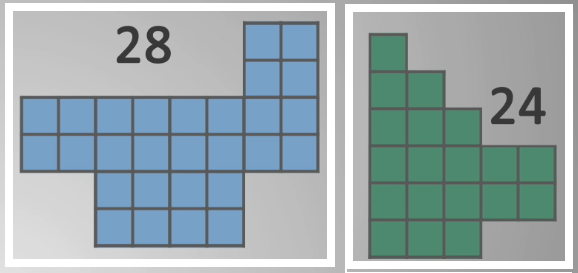
Эта мерка также подходит к синей фигуре. Считаем, в синей фигуре уместилось 28 мерок, а в зелёной фигуре только 24. Получается, что площадь зелёной фигуры меньше площади синей на 4 мерки. Способом подбора мерок мы нашли вариант, который в равной степени подходит для измерения площадей обеих фигур.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!