
На рисунке изображены геометрические фигуры: треугольники, круги, четырехугольники, квадраты. Все они разные по размеру. Вы легко сможете определить на глаз, какая из этих фигур имеет самый большой размер, а какая – самый маленький.
Гораздо сложнее сравнить фигуры, имеющие небольшую разницу в размерах, или фигуры, отличающиеся формой.
Чтобы сравнить их между собой, достаточно просто наложить одну на другую. Это приводит нас к выводу: квадрат больше круга. Второй способ: переведём на прозрачный лист бумаги фигуру и накладываем её на другую фигуру: овал оказывается больше прямоугольника.
Говоря о размерах геометрических фигур, мы имеем в виду хорошо известные величины: длина, ширина. В данном случае мы сравнивали поверхности фигур, мысленно проводя по ним ладонью. Новая величина для определения размеров фигуры называется площадью.

Говорят, что площадь квадрата больше площади круга, а площадь круга меньше площади квадрата и, аналогично, площадь овала больше площади прямоугольника, а площадь прямоугольника меньше площади овала.
Таким образом, для того, чтобы сравнить площади фигур, надо одну из них наложить на другую.
В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой S.
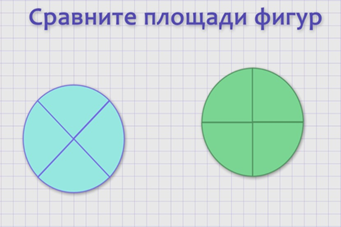
Попробуйте сравнить площади данных фигур.
Обратите внимание, фигуры разделены на равные части. Сосчитаем, сколько частей образуют первую фигуру. Их 4. Вторая фигура также состоит из 4-х частей, но её части расположены по-другому. Таким образом, мы можем утверждать, что данные фигуры состоят из равного количества одинаковых частей. Такие фигуры называются равносоставленными.
Равносоставленные фигуры имеют одинаковую площадь. А вот форма равносоставленных фигур может быть разнообразной.
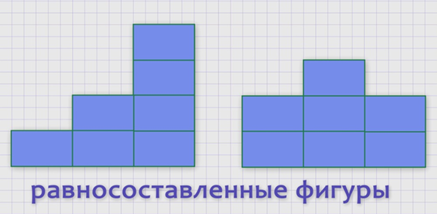
Итак, для того, чтобы получить равносоставленные фигуры, необходимо выполнить два условия:
во-первых, все части фигур должны иметь одинаковые размеры и форму;
во-вторых, количество частей также должно быть одинаковым.
Что произойдёт, если не выполнить одно из условий? Например, некоторые части фигуры изменили свой размер. Площадь фигуры заметно увеличилась.
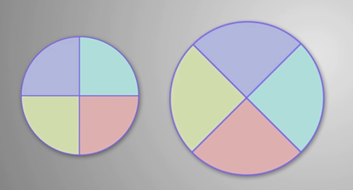
Сейчас мы уже не можем утверждать, что данные фигуры имеют одинаковую площадь.
А если изменить количество частей?
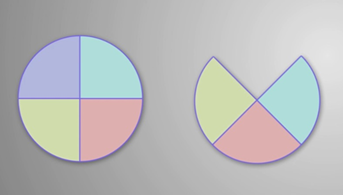
Фигура заметно уменьшилась в размере. Площади этих фигур также нельзя считать одинаковыми.
Итак, подведем итог нашим рассуждениям: площади фигур (или предметов в окружающем мире) можно сравнивать разными способами. Наш глазомер легко справляется с простыми случаями сравнения площадей, например, площадь пола в вашем классе намного меньше площади пола в спортзале вашей школы!


Если нам нужно сравнить площади (размеры), например, двух похожих вещей, мы будем аккуратно накладывать их друг на друга. А если вам, как Тому Сойеру, придётся красить забор и сравнивать его с площадью забора, который покрасил ваш друг, то здесь не обойтись без сравнения количества одинаковых частей – досочек!
А вдруг ваши заборы окажутся равносоставленными фигурами?
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!