На этом уроке вы узнаете о понятии десятичной дроби, познакомитесь с ее историей, научитесь читать и записывать десятичные дроби, переводить обыкновенную дробь со знаменателем 10, 100,1000 и т.д. в десятичную и наоборот.
Итак, что же такое десятичная дробь? Оказывается, это форма записи обыкновенной дроби, у которой в знаменателе стоит 10, 100, 1000, 10000 и так далее, т.е. 1 с несколькими нулями. Сначала пишут целую часть, затем числитель дробной части, и целую часть от дробной, отделяют запятой.
Например, 12 целых 7 десятых записывают в виде 12,7. Другой пример: 8 целых 156 тысячных равно 8,156. А как же быть, если целая часть отсутствует? Т. е. дробь правильная? Тогда целую часть записывают в виде 0! Например, 17 сотых = 0,17.
Внимание! Чтобы правильно записать десятичную дробь, числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе дробной части. Таким образом, дробь
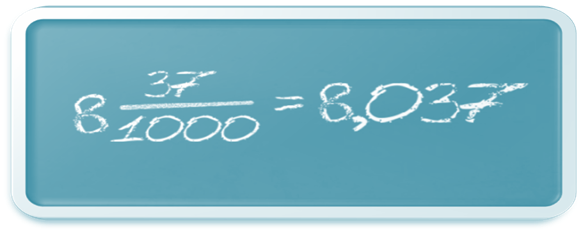
Другой пример: как записать в десятичной записи дробь 3 миллионных?


Чтобы правильно читать десятичные дроби, необходимо запомнить, как называется каждый разряд в дробной части. На первом месте после запятой пишутся десятые доли, на втором – сотые, дальше тысячные, потом десятитысячные, затем стотысячные и т.д.
Например, вот это число (1234,5678 ) читается так: 1234 целых 5678 десятитысячных.
Теперь вы знаете, как переводить обыкновенную дробь в десятичную. А как же наоборот? Тоже достаточно просто! К примеру, десятичную дробь 1,5 прочитаем, как одна целая пять десятых и можно записать так:
![]()
дробь 1,05 читается как одна целая пять сотых и записывается как: 1
![]()
а дробь 1 ,005 читается как одна целая пять тысячных и запишется как:
![]()
Оказывается, уже в древнем Китае пользовались десятичной системой мер и обозначали дробь словами, используя меры длины: чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки.
Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков. Затем в 15 веке крупный ученый того времени Джемшид Гиясэддин аль – Каши впервые изложил учение о десятичных дробях, он ввел новую запись для десятичных дробей, когда целая и дробная части пишутся в одну строку и отделяются друг от друга либо вертикальной чертой, либо чернилами разных цветов. Примерно в то же время математики Европы пытались найти удобную запись десятичной дроби. 
 В книге «Математический канон» французский математик Франсуа Виет в записи десятичной дроби дробную часть подчеркивал и записывал выше строки целой части числа. В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого. Запятая же в записи дробей впервые встречается в 1592г., а в 1617г. шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой. Современную запись десятичных Иоганн Кеплердробей, т.е. отделение целой части от дробной запятой, предложил Иоганн Кеплер. В странах, где говорят по английский и в настоящее время вместо запятой пишут точку.
В книге «Математический канон» французский математик Франсуа Виет в записи десятичной дроби дробную часть подчеркивал и записывал выше строки целой части числа. В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого. Запятая же в записи дробей впервые встречается в 1592г., а в 1617г. шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой. Современную запись десятичных Иоганн Кеплердробей, т.е. отделение целой части от дробной запятой, предложил Иоганн Кеплер. В странах, где говорят по английский и в настоящее время вместо запятой пишут точку.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!