Существует несколько способов решения текстовых задач:

• арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;

• алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;

• геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;

• схематический способ – это способ решения текстовой задачи с помощью схем;

• графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.

Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели. В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи. В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи. В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры. В схематическом способе математической моделью является схема, с помощью которой находят решение задачи. В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.

На этом занятии мы рассмотрим схематический способ решения текстовой задачи. Это старинный приём решения задач. Его знали в Древней Греции ещё до нашей эры во времена Пифагора. А в 18-19 веках нашей эры этот метод успешно использовали купцы при торговле смешанным товаром. Схематический способ предполагает решение текстовой задачи с помощью схемы. Познакомимся с ним на примере следующей задачи.

Задача 1. Родительский комитет детского садика решил закупить конфеты для формирования новогодних подарков для 100 детей. Было решено сделать подарки на сумму 150 рублей каждый. На оптовой базе они выбрали конфеты по цене 225 рублей, 135 рублей и 180 рублей за 1кг. Каждая конфета в среднем весит 10г. Сколько конфет каждого вида необходимо купить родительскому комитету?

Решение:

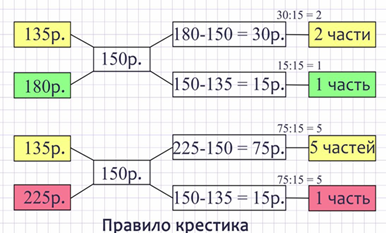
Решим задачу схематическим способом Леонтия Филипповича Магницкого для трёх веществ. Математик Магницкий - автор первого в России учебного справочника по математике. Запишем в столбик друг под другом цены двух сортов конфет в порядке возрастания 135руб и 180руб. В центре второго столбика рядом запишем цену смеси конфет 150руб. В третьем столбце сверху запишем разность 180 и 150, а ниже разность 150 и 135.

Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 150-ти, то есть 30руб и 15руб, Разделим эти числа на их наибольший общий делитель – на 15, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 2части и 1часть. Теперь аналогичную операцию проделаем с конфетами по цене 135руб и 225руб. В центре второго столбика рядом запишем цену смеси конфет 150руб. В третьем столбце сверху запишем разность 225 и 150, а ниже разность 150 и 135. Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 150-ти, то есть 75руб и 15руб, Разделим эти числа на их наибольший общий делитель – на 15, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 5частей и 1часть. Мы получили две схемы, в которых результаты разностей чисел мы записывали крестиком относительно стоимости смеси 150рублей. Именно поэтому этот способ по-другому называется «правилом крестика». Числа четвёртых столбцов схем показывают долю конфет соответствующей цены от общего количества конфет в подарке по цене 150рублей за 1кг. Из схемы видно, что в смеси на конфеты по цене 135руб приходится 2 + 5частей, то есть 7частей, а на конфеты по цене 180руб и 225руб приходится по 1части. Это означает, что если на 100детей распределить по 1конфете массой 10г, то потребуется 1кг конфет по 180руб и 1кг по 225руб. Конфет по цене 135руб должно быть в 7 раза больше, значит, нужно закупить 7кг конфет по этой цене.

Схематический способ решения текстовых задач значительно упрощает решение задач на смешивание растворов и получение сплавов определённого долевого или процентного состава. Рассмотрим следующую задачу.

Задача 2.

У хозяйки имеются 70%-ная уксусная эссенция и 6%-ный раствор пищевого уксуса, купленные в магазине. Для консервирования ей нужен 14%-ный раствор уксуса. Как хозяйке получить необходимый раствор?

Решение:

Запишем в столбик друг под другом проценты смешиваемых растворов в порядке возрастания 6% и 70%. В центре второго столбика рядом запишем процент нового раствора 14%. В третьем столбце сверху вниз запишем разность числа последней строки и 14, а затем разность 14 и числа первой строки. Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 14-ти, то есть 56% и 8%. Разделим эти числа на их наибольший общий делитель – на 8, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 7 и 1. Эти числа определяют долю раствора соответствующей концентрации от общего количества раствора. Таким образом, чтобы получить

14 % – ный раствор уксуса, надо смешать одну часть эссенции и 7 частей пищевого уксуса. В роли одной части может выступать любой объём. Хозяйка пипеткой может взять 1 каплю эссенции и 7капель уксуса, если ей нужен небольшой объём. Для объёма побольше можно взять, например, чайную ложку эссенции и 7чайных ложек уксуса.

Разберём решение ещё одной задачи на сплавы схематическим способом.

Задача 3.

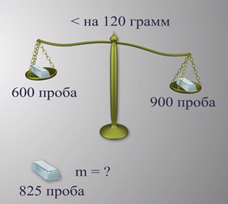
Масса одного куска серебра 600-й пробы отличается от массы куска серебра 900-й пробы на 120 граммов. Определить массу слитка из этих кусков, если его проба стала равна 825.

Решение:

Запишем в столбик друг под другом пробы кусков серебра в порядке возрастания 600 и 900. В центре второго столбика рядом запишем пробу нового сплава из этих кусков 825. В третьем столбце сверху вниз запишем разность числа последней строки и 825, а затем разность 825 и числа первой строки. Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 825-ти, то есть 75 и 225. Разделим эти числа на их наибольший общий делитель – на 75, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 1 и 3. Эти числа определяют долю куска серебра соответствующей пробы от общей массы сплава из кусков серебра 600-й и 900-й пробы. По условию задачи массы кусков серебра отличаются друг от друга на 120 г. Из схемы видно,куски отличаются друг от друга на 2 части, следовательно, на 1 часть приходится 120:2 г, то есть 60 г. Главный вопрос задачи: определить массу слитка из кусков серебра. Из схемы видно, что на весь сплав приходится 4 части. Нетрудно понять, что вся масса слитка в 2 раза больше разности масс двух кусков серебра, значит, вся масса слитка будет составлять 2 умноженное на 120 г или 4 умноженное на 60 г, то есть 240 г.

Таким образом, из приведённых примеров различных задач можно сделать вывод, что схематический способ решения текстовых задач значительно упрощает их решение. Недостатком этого метода является ограниченность его применения. Таким способом можно решать только задачи на смешивание сыпучих материалов, на разбавление растворов или на сплавы металлов.