В этом уроке узнаем, какой угол называется центральным углом, какой – вписанным, поговорим о дугах окружности, в чем они измеряются, познакомимся с теоремой о вписанном угле и её следствиями, рассмотрим решение задачи по теме урока.
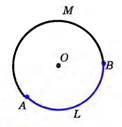
Если на окружности отметить две точки А и В, то они разделят окружность на две дуги. Чтобы различать эти дуги друг от друга, между точками А и В отмечают дополнительные точки, например М и L.
В геометрии дуги обозначают так: ⌣АМВ и ⌣АLВ.
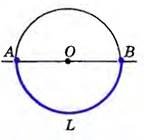
Любой диаметр делит окружность на две дуги, эти дуги называют полуокружностями.
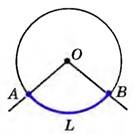
Угол с вершиной в центре окружности называется центральным углом окружности.
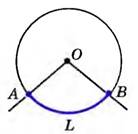
На рисунке угол АОВ – центральный, так как его вершиной является центр окружности.
Дуга окружности измеряется в градусах.
Если дуга окружности меньше полуокружности или является полуокружностью, то ее градусная мера равна градусной мере центрального угла.
На этом рисунке дуга окружности меньше полуокружности – градусная мера дуги АLВ равна градусной мере центрального угла АОВ: ⌣АLВ = ∠АОВ.
На другом рисунке дуга окружности является полуокружностью – градусная мера дуги АLВ равна градусной мере центрального угла, который является развернутым, а значит равен 180°. Значит, градусная мера полуокружности равна 180°.
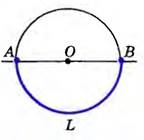
Если дуга больше полуокружности, то ее градусная мера равна разности 360° и градусной меры центрального угла: ⌣АМВ = 360° – ∠АОВ.
Перейдем к рассмотрению понятия «вписанный угол».
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называют вписанным углом.
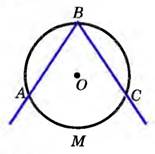
На рисунке угол АВС – вписанный, так как его вершина лежит на окружности, а стороны пересекают её. Внутри этого угла расположена дуга АМС.
Говорят, что вписанный угол АВС опирается на дугу АМС.
Докажем теорему о вписанном угле.
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Дано:
∠АВС – вписанный угол окружности с центром в точке О, опирающийся на дугу АС.
Доказать:
Угол АВС равен половине дуги АС, т.е. ∠АВС = ½⌣АС
Доказательство:
Для доказательства необходимо рассмотреть три возможных случая расположения луча ВО относительно угла АВС.
1 Случай:
Луч ВО совпадает с одной из сторон угла АВС, например со стороной ВС.
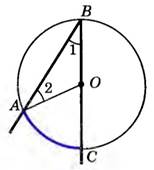
Тогда дуга АС меньше полуокружности, поэтому центральный угол АОС равен градусной мере дуги АС: ∠АОС = ⌣АС
Угол АОС – внешний угол треугольника АОВ, а внешний угол треугольника по свойству равен сумме углов треугольника, не смежных с ним, т.е. ∠АОС = ∠1 + ∠2 .
Треугольник АОВ равнобедренный (ОА и ОВ – радиусы одной и той же окружности), а в равнобедренном треугольнике углы при основании равны, т.е. ∠1 = ∠2.
А значит ∠АОС = ∠1 + ∠2 = 2∠1.
Отсюда следует 2∠1 = ⌣АС, или ∠АВС = ∠1 = ½⌣АС.
2 Случай:
Луч ВО делит угол АВС на два угла.
Тогда луч ВО пересекает дугу АС в некоторой точке D.
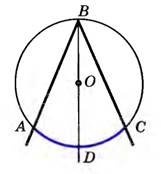
Эта точка делит дугу АС на две дуги: ⌣АD и ⌣DС.
Из доказанного 1 случая для вписанных углов АВD и DВС будут иметь место равенства: ∠АВD = ½⌣АD и ∠DВС = ½⌣DС.
Складывая, получим
∠АВС = ∠АВD + ∠DВС = ½⌣АD + ½⌣DС = ½⌣АС.
3 Случай:
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
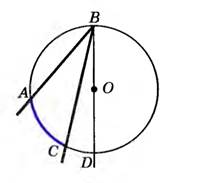
Тогда ∠АВС = ∠АВD – ∠DВС = ½⌣АD – ½⌣DС = ½⌣АС.
Что и требовалось доказать.
Из теоремы о вписанном угле вытекают два следствия.
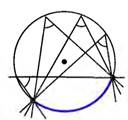
Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
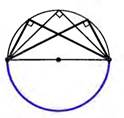
Следствие 2.
Вписанный угол, опирающийся на полуокружность – прямой.
Следствие 1 позволяет доказать теорему о произведении отрезков пересекающихся хорд.
Теорема:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
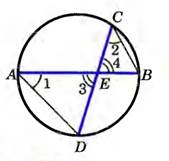
Дано:
Окружность, АВ и СD – хорды, пересекающиеся в точке Е.
Доказать:
АЕ · ВЕ = СЕ · DЕ
Доказательство:
Рассмотрим треугольники АЕD и СЕВ.
∠1 = ∠2, так как данные углы вписанные и опираются на одну и ту же дугу ВD;
∠3 = ∠4, как вертикальные углы,
Значит треугольники АЕD и СЕВ подобны по первому признаку подобия треугольников.
У подобных треугольников сходственные стороны пропорциональны, т.е.
![]()
Теорема доказана.
Рассмотрим решение задачи.
Задача:
Хорды АВ и СD пересекаются в точке Е.
Длина отрезка АЕ = 9 см, СЕ = 8 см.
Длина отрезка ЕD на 5 см больше длины отрезка ВЕ.
Найдите длины хорд АВ и СD.
Дано:
Окружность
АВ и СD – хорды
АВ∩СD = Е
АЕ = 9 см
СЕ = 8 см
ЕD>ВЕ на 5 см
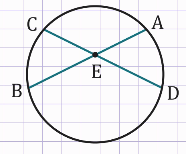
Найти:
АВ, СD
Решение:
Для решения задачи используем теорему о произведении отрезков пересекающихся хорд, т.е. АЕ · ВЕ = СЕ · DЕ.
Пусть ВЕ = х, тогда ЕD = х + 5.
Подставим данные в равенство АЕ · ВЕ = СЕ · DЕ, получим 9х = 8(х + 5).
Решив уравнение, получим х = 40 см, т.е. ВЕ = 40 см, ЕD = 45 см.
Тогда хорда АВ = АЕ + ВЕ = 9 + 40 = 49 см, СD = СЕ + ЕD = 8 + 45 = 53 см.
Ответ:
АВ = 49 см, СD = 53 см.
В этом уроке Вы познакомились с центральными и вписанными углами, доказали теорему о вписанном угле и теорему о произведении отрезков пересекающихся хорд, а также рассмотрели решение задачи по теме урока.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!