§ 1  Теорема о биссектрисе угла

С любым треугольником в геометрии связаны четыре точки:

1) точка пересечения медиан;

2) точка пересечения биссектрис;

3) точка пересечения высот (или их продолжений);

4) точка пересечения серединных перпендикуляров к сторонам.

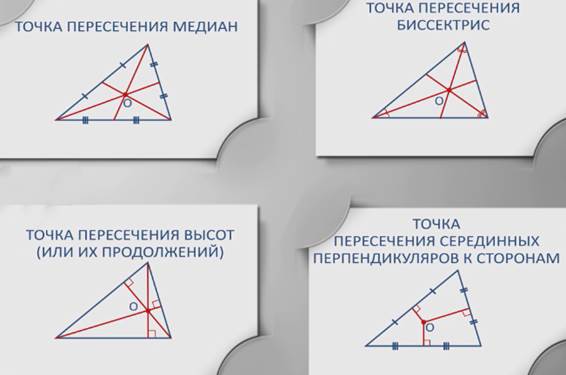
Эти четыре точки называют замечательными точками треугольника.

В этом уроке рассмотрим и докажем теоремы, следствия из этих теорем, связанные с замечательными точками треугольника, и рассмотрим их применение при решении задач.

Познакомимся сначала с теоремой о биссектрисе угла.

Теорема:

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Обратно:

Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Докажем эти утверждения.

Дано:

∠ВАС, АМ – биссектриса, МК и МL перпендикулярны к прямым АВ и АС.

Доказать:

МК = МL

Доказательство:

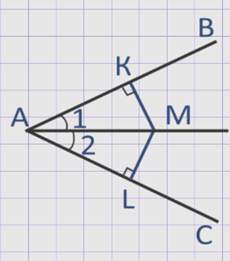
Рассмотрим прямоугольные треугольники АКМ и АLМ.

Они равны по гипотенузе и острому углу (АМ – общая сторона, ∠1 = ∠2 , так как по условию АМ – биссектриса).

Из равенства треугольников следует МК = МL.

Теперь докажем обратное утверждение.

Дано:

∠ВАС, точка М лежит внутри угла и равноудалена от сторон угла АВ и АС.

Доказать:

луч АМ – биссектриса ∠ВАС.

Доказательство:

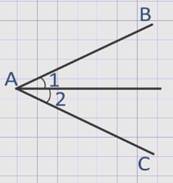
Проведем перпендикуляры МК и МL к прямым АВ и АС.

Прямоугольные треугольники АМК и АМL равны по гипотенузе и катету (АМ – общая гипотенуза, МК = МL по условию).

Следовательно, ∠1 = ∠2, это означает, что луч АМ – биссектриса ∠ВАС.

Теорема доказана.

Из утверждения теоремы следует еще одно утверждение.

Следствие: биссектрисы треугольника пересекаются в одной точке.

§ 2  Теорема о серединном перпендикуляре к отрезку

Перейдем к теореме о серединном перпендикуляре к отрезку.

Но сначала дадим определение.

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

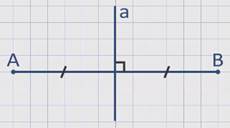
На рисунке прямая а является серединным перпендикуляром к отрезку АВ.

Теорема:

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно:

Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Дано:

АВ – отрезок, прямая m – серединный перпендикуляр к отрезку АВ, точка О – середина этого отрезка.

М – произвольная точка прямой m.

Доказать: АМ = ВМ

Доказательство:

Если точка М совпадает с точкой О, то равенство АМ = ВМ верно.

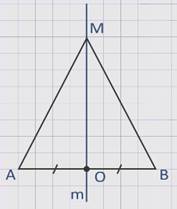
Пусть М и О – различные точки.

Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ по условию, ОМ – общий катет), из равенства треугольников следует, что АМ = ВМ.

Докажем обратное утверждение.

Дано:

АВ – отрезок, N – произвольная точка такая, что АN = ВN.

Доказать:

точка N лежит на прямой m – серединном перпендикуляре к АВ.

Доказательство:

если точка N – точка прямой АВ, то она совпадает с серединой О отрезка АВ и потому лежит на прямой m.

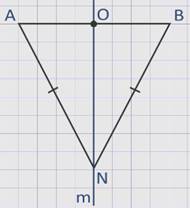
Если же точка N не лежит на прямой АВ, то треугольник АNВ – равнобедренный, так как АN = ВN.

Отрезок NО является медианой равнобедренного треугольника, значит, она является и его высотой.

Таким образом, NО перпендикулярен АВ, поэтому прямые ОN и m совпадают, т.е. точка N – точка прямой m.

Теорема доказана.

Следствием доказанной теоремы является следующее утверждение.

Следствие: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

§ 3  Теорема о пересечении высот теугольника

Рассмотрим еще одну теорему о пересечении высот треугольника.

Теорема:

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Дано:

АА1 , ВВ1, СС1 – высоты треугольника АВС.

Доказать:

АА1 , ВВ1, СС1 пересекаются в точке О.

Доказательство:

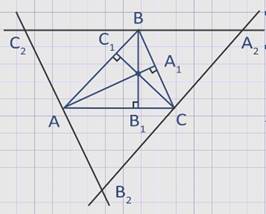
Проведем через вершины А, В и С прямые, параллельные противоположным сторонам треугольника.

Получим треугольник А2В2С2.

Точки А, В, С являются серединами треугольника А2В2С2.

Действительно, в параллелограммах АВА2Си АВСВ2 противоположные стороны равны, т.е. АВ = А2С, АВ = СВ2 , поэтому А2С = СВ2.

Аналогично С2А = АВ2 и С2В = ВА2.

Из построения следует, что СС2 перпендикулярно А2В2, АА1 перпендикулярно В2С2, ВВ1 перпендикулярно А2С2.

Таким образом, прямые АА1, ВВ1, СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2, следовательно, они пересекаются в одной точке.

Теорема доказана.

Решим задачу, используя полученные знания.

Задача.

В треугольнике АВС проведены высоты АК и ВD, пересекающиеся в точке О.

Угол САВ = 42°.

Найдите величину угла АСО.

Дано:

∆АВС, АК и ВD – высоты треугольника АВС, пересекающиеся в точке О, ∠САВ = 42°

Найти:

∠АСО.

Решение:

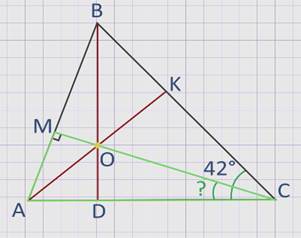
для вычисления угла АСО проведем еще одну высоту СМ треугольника АВС, по теореме о пересечении высот треугольника высота СМ пройдет через точку О, а значит, треугольник АСМ – прямоугольный.

Тогда ∠АСО = 180° – (90° + 42°) = 48°.

В этом уроке познакомились с замечательными точками треугольника, рассмотрели теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку и их следствия, теорему о пересечении высот (или их продолжений), а также рассмотрели решение задачи по теме урока.