На этом уроке Вы узнаете, что называют разностью двух чисел, а также рассмотрите действие вычитания чисел, на координатном луче.

Давайте решим следующую задачу:

Турист прошел за 3 часа 10 км. Сколько он прошел за третий час своего путешествия, если за первые два часа он преодолел 7 км?

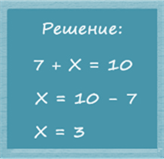
Решение: в этой задаче число 10 является суммой двух чисел, одно из которых равно 7, а другое неизвестно.

Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое, называют вычитанием. В данной задаче 7 + 3 = 10, значит искомое слагаемое равно трем. Т.е. за третий час турист прошел 3 км. Пишут следующим образом: 10 – 7 = 3.

Число, из которого вычитают, называют уменьшаемым. Число, которое вычитают, называют вычитаемым. А результат вычитания называют разностью.

Вернемся к задаче про туриста. При вычитании 10 – 7 = 3, число 10 – это уменьшаемое, число 7 – это вычитаемое, число 3 – это разность.

Важно отметить, что при действии вычитания с натуральными числами уменьшаемое не может быть меньше вычитаемого. Так как разность двух чисел показывает, на сколько первое число больше второго, другими словами, на сколько второе число меньше первого, или же вычитаемое меньше уменьшаемого. Например, 11 – 6 = 5, уменьшаемое 11 больше вычитаемого 6 на разность 5.

Давайте посмотрим, как же можно производить вычитание чисел с помощью координатного луча. Начертим координатный луч с началом в точке О и единичным отрезком равным одной клетке. Для удобства расположим его горизонтально слева направо.

Вычитание из натурального числа a натурального числа в на координатном луче можно истолковать следующим образом:

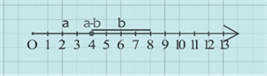
сначала находим точку, координатной которой является уменьшаемое а. Теперь из этой точки в направлении точки O последовательно друг за другом необходимо отложить единичные отрезки в том количестве, которое равно вычитаемому в. Последовательность этих действий приведет нас в точку на координатном луче, координата которой равна разности а-в.

Таким образом, можно сделать вывод, что вычитание из натурального числа а натурального числа в на координатном луче представляет собой не что иное, как перемещение влево из точки с координатой а на расстояние в, при этом мы попадаем в точку с координатой а-в. Например, перед вами рисунок, который иллюстрирует вычитание из натурального числа 6 натурального числа 4 на координатном луче. После выполнения необходимых действий попадаем в точку с координатой 2, т.е. 6 – 4 = 2.

Кстати, чтобы правильно прочитать разность можно употреблять два глагола: вычесть или отнять, но здесь важно следить за верным сочетанием глаголов и предлогов.

Глагол вычесть требует предлога из. Глагол отнять требует предлога от.

Например, из ста двадцати вычесть сорок девять. Или же от ста двадцати отнять сорок девять.