В этом уроке Вы познакомитесь с новым понятием – прямоугольный параллелепипед, кроме того научитесь вычислять площадь его поверхности.
Итак, что же такое прямоугольный параллелепипед? Это такая объемная фигура, которая состоит из 6 прямоугольников, каждый из которых называют гранью прямоугольного параллелепипеда.
Многие предметы окружающие нас в повседневной жизни имеют форму параллелепипеда. Например, кирпич, спичечный коробок, дом – небоскреб прямоугольной формы, коробка из-под телевизора или системный блок компьютера, все они служат примерами прямоугольного параллелепипеда.
Таким образом:
1.Прямоугольный параллелепипед имеет 6 граней – прямоугольников.
2.Противоположные грани его попарно равны.
3.стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда. Всего у параллелепипеда имеется 12 ребер и 8 вершин.
4.Любой прямоугольный параллелепипед имеет три измерения – длину, ширину, высоту. Обычно за них принимают длины трех рёбер прямоугольного параллелепипеда, имеющих общий конец, то есть выходящих из одной вершины.
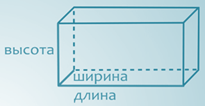
Так вот, если все три измерения равны, то такой прямоугольный параллелепипед называют кубом. Поэтому, не трудно догадаться, что поверхность куба состоит из 6 равных квадратов, кроме того все 12 рёбер куба также равны.
Давайте решим такую задачу. Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3 см, 6 см и 10 см.
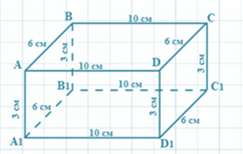
Решение:
![]()
Т.к. прямоугольный параллелепипед имеет 6 граней – прямоугольников, причем противоположные грани его попарно равны, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей его 6 граней, при этом площади противоположных друг другу граней будут равны.
Поэтому найдем сначала площади граней, начнем с прямоугольника, у которого стороны равны 3 см и 6 см (помним, что таких граней в параллелепипеде две).
![]()

Для этого 3 умножим на 6, получим 18 квадратных сантиметров. Теперь перейдем к двум другим одинаковым граням – прямоугольникам, со сторонами 3 см и 10 см. Площадь каждой из них равна 3 умножить на 10, будет 30 квадратных сантиметров. Теперь осталось найти площадь каждой из двух последних одинаковых граней со сторонами 6 см и 10 см. Умножим 6 на 10, получим 60 квадратных сантиметров. Значит, площадь всей поверхности прямоугольного параллелепипеда равна 2 умножить на 18 плюс 2 умноженное на 30 плюс 2 умноженное на 60, равно 36 + 60 + 120, получится 216.
Ответ: площадь поверхности прямоугольного параллелепипеда равна двести шестнадцать квадратных сантиметров.
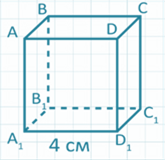
Выполним следующее задание: найти площадь поверхности куба с ребром 4 см.
![]()
Решение: так как у куба 6 граней, каждая из которых является квадратом со стороной 4 см, значит, найдем сначала площадь одной грани. Для этого 4 умножим на 4, или 4 возведем в квадрат, получим 16.
![]()
А затем 16 умножим на 6, будет 96. Ответ: площадь поверхности куба 96 квадратных сантиметров.
Таким образом, на этом уроке Вы познакомились с таким понятием как прямоугольный параллелепипед, его элементами – гранями, ребрами, вершинами. Узнали, что куб – это прямоугольный параллелепипед, у которого все измерения равны. А также научились находить площади поверхностей прямоугольного параллелепипеда и куба.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!