В этом уроке рассмотрим деление натуральных чисел с остатком. Вы познакомитесь с такими понятиями как неполное частное и остаток, научитесь находить делимое по неполному частному, делителю и остатку.

Что такое деление, вы уже знаете, это действие, с помощью которого по произведению и одному из множителей находят другой множитель. Но разделить одно натуральное число на другое нацело не всегда возможно.

Например, решим такую задачу:

Четверо друзей купили коробку конфет, в ней оказалось 23 штуки. По сколько конфет получит каждый из друзей, если разделить их между ними поровну?

Если конфет было бы 20, то каждый получил бы по 5, так как 20 разделить на 4, будет 5. Но в коробке 23 конфеты, значит еще 3 конфеты останутся. Вот и получается деление с остатком числа 23 на 4:

23 : 4 = 5 (ост.3 ).

В этой записи число 23 – делимое, число 4 – делитель, число 5 – неполное частное, число 3 – остаток.

Важно отметить, что при делении с остатком, остаток должен быть всегда меньше делителя. В нашем примере 3 меньше 4.

А может ли остаток быть равным нулю? Да!

В этом случае говорят, что делимое делится на делитель без остатка, т.е. нацело. Например, 42 : 14 = 3, здесь остаток равен 0, т.е. разделили нацело.

А какие остатки, например, может иметь число 7? 0, 1, 2, 3, 4, 5 и 6. Т.е. все числа, меньшие 7.

Вернемся к задаче, как же себя проверить, правильно ли мы ее решили?

Так как 4 друга получили по 5 конфет, значит 4 умножить на 5 будет 20, да еще 3 конфеты остались в коробке, значит 20 + 3 = 23.

Таким образом, получили правило:

Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.

Например:

Найдите делимое, если делитель равен 25, неполное частное 2, остаток 12.

Используя правило для нахождения делимого при делении с остатком, нужно неполное частное 2 умножить на делитель 25, будет 50, и к полученному произведению прибавить остаток 12, т.е. 50 + 12 = 62. Ответ: делимое равно 62.

Следующее задание:

Выполните деление с остатком и назовите делимое, делитель, неполное частное и остаток – 384 разделить на 10.

Решение:

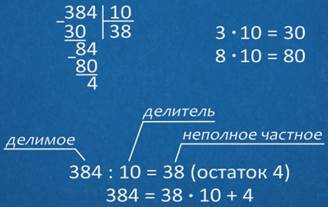
Выполняем деление в столбик 384 разделить на 10, берем по 3, 3 умножить на 10, будет 30, из 38 вычесть 30, получаем 8, сносим 4, имеем 84 разделить на 10, берем по 8, 8 умножить на 10, будет 80, из 84 вычесть 80, получаем 4, деление окончено.

Итак, при делении трехсот восьмидесяти четырех на 10, получили 38 и в остатке 4,

Здесь делимое – это 384, делитель – 10, неполное частное – 38, остаток – 4.

Таким образом, на этом уроке мы рассмотрели несколько примеров деления с остатком и научились определять делимое, делитель, неполное частное и остаток.