В этом уроке рассмотрим правило деления десятичных дробей на натуральные числа, а также научимся легко и быстро делить на 10, 100, 1000 и т.д.
Для начала давайте решим задачу:
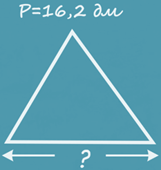
Периметр равностороннего треугольника равен 16,2 дм.
Какова длина стороны треугольника?
Вы знаете, что равносторонним называют тот треугольник, у которого все стороны равны. Для того, чтобы решить эту задачу, необходимо 16,2 разделить на 3.
Переведем 16,2 дм в сантиметры, получим 162 см.
Теперь разделим 162 на 3, получим 54 см.
Переводим обратно в дециметры, т.е. 5,4 дм.
Значит, при делении 16,2 на 3 будет 5,4.
И в самом деле, если умножить 5,4 на 3, то получится 16,2.
Давайте определимся, что значит, разделить десятичную дробь на натуральное число?
Это значит найти такую дробь, которая при умножении на это натуральное число дает делимое.
Для деления десятичной дроби на натуральное число существует следующее правило:
1. Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
2. Ставим в частном запятую, когда заканчивается деление целой части делимого.
Внимание! Если целая часть делимого меньше делителя, то в частном ставим 0 целых.
Давайте вернемся к нашей задаче:
Рассмотрим деление 16,2 на 3 столбиком:

делим 16 на 3, берем по 5, получаем 3 умножить на 5, будет 15, вычитаем 15 из 16, останется 1. Далее закончилось деление целой части, поэтому в частном мы должны поставить запятую. Теперь, не обращая внимания на запятую, сносим 2, получается 12, делим на 3, берем по 4, значит 3 умножаем на 4, будет 12, и из 12 вычитаем 12, будет ноль. Значит, деление закончилось и ответ при делении 16,2 на 3 равен 5,4.
Рассмотрим другой пример: 0,806 разделить на 31.
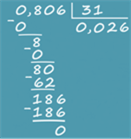
Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31).
Поэтому в частном сразу ставим 0 в целой части, отделив ее запятой. Затем начинаем делить по правилам деления столбиком, не обращая внимания на запятую.
Итак, следующая цифра 8, опять меньше делителя, значит после запятой снова записываем ноль. Затем берем в рассмотрение 80, после нуля в частномзаписываем 2, умножаем 2 на 31, получаем 62, из 80 вычитаем 62, будет 18, сносим шестерку, имеем 186, значит в частном после 2 записываем шестерку. 6 умножить на 31, получается 186, таким образом ответ готов: 0,026.
А теперь давайте разделим 87,3 на 10.
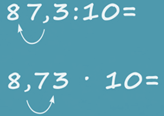
Если полученное частное умножить на 10, должно получиться снова 87,3. Но при умножении десятичной дроби на 10 запятую переносят на одну цифру вправо. Значит, при делении на 10 запятую надо переносить на одну цифру влево: 87,3 разделить на 10 будет 8,73. Проверка: 8,73 • 10 получится 87,3.
Как Вы считаете, на сколько знаков влево надо перенести запятую при делении на 100? Правильно! На 2 знака.
Итак, получили следующее правило:
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д. надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе. При этом иногда приходится написать перед целой частью нуль или несколько нулей.
Рассмотрим два примера.
Первый: 213,84 нужно разделить на 10. Количество нулей после единицы равно одному, значит, запятая переносится влево на один знак и получится 21,384.
Второй пример: 8,765 нужно разделить на 100. Нулей после единицы два, значит, запятую надо перенести влево на два знака, для этого необходимо дописать нужное количество нулей, т.е. припишем перед восьмеркой два нуля 008,765 и разделим на 100, перенесем запятую влево на два знака, получится 0,08765.
Таким образом, в этом уроке мы выяснили, как делить десятичную дробь на натуральное число, а также получили правило, которое позволяет очень легко и быстро разделить десятичную дробь на 10, 100, 1000 и т.д.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!