Многогранники являются геометрическими фигурами, красота и гармония которых видна даже тем, кто очень далек от математики. Многогранники окружают нас в жизни повсюду. Их создают люди своими руками, их создает природа. На занятии мы поговорим об особой группе многогранников – о правильных многогранниках.
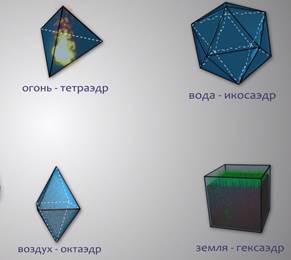
Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической геометрии к философской. Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики – это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалась способность защищать человека от злых духов. Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем и Платон полагали, что материя состоит их четырех основных элементов: огня, земли, воздуха и воды. В последствие правильные многогранники стали называть Платоновыми телами. Согласно учению древних, атомы основных элементов должны иметь форму различных Платоновых тел: огонь – тетраэдр, вода – икосаэдр, воздух – октаэдр, земля – гексаэдр, вселенная – додекаэдр.
Дадим определение правильного многогранника, чтобы было удобно оперировать математическими понятиями при изучении этих особенных пространственных тел. Многоугольник называется правильным, если у него равны стороны и углы. Примерно так же определяют правильные многогранники. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и двугранные углы при всех ребрах равны между собой. Существует и другое определение правильного многогранника. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер. Оба эти определения используются в математике как равноправные.
Правильных многоугольников бесконечно много: при каждом n больше или равного трем имеется правильный n-угольник (причем только один с точностью до подобия). Правильных многогранников всего пять, и два из них мы уже знаем – это тетраэдр и куб, который носит имя гексаэдр в ряду правильных многогранников. Каждый из такого рода многогранников имеет свое, отличное от других количество граней, поэтому и названия они когда-то получили благодаря этим числам: тетраэдр (4 грани, от греческого «тетра» - четыре и «хендрон» - основание, грань), гексаэдр (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).
Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n больше или равного шести. Итак, угол правильного многоугольника при n больше или равном шести, не меньше 120 градусов. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n больше или равном 6, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем 120 градусов *3 = 360 градусам. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360 градусов. Что и требовалось доказать! Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n больше или равного шести. Напрашивается вывод. Каждая вершина правильного многогранника может быть вершиной либо трех, четырех или пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников. Других вариантов не существует.
Рассмотрим более подробно многогранники, которые мы сегодня изучаем.

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой его вершине равна 180 градусам. Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240 градусов. Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 градусов.
Гексаэдр (или как его часто называют – куб) составлен из шести квадратов. Каждая вершина гексаэдра является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 градусов. Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 градусам.
Полученные знания можно упорядочить в таблице, в строках которой расположены правильные многогранники, а в столбцах их характеристики.
|
Изображение |
Правильный многогранник |
Число сторон у грани |
Число рёбер, примыкающих к вершине |
Число вершин |
Число рёбер |
Число граней |
|
3 |
3 |
4 |
6 |
4 |
||
|
3 |
4 |
6 |
12 |
8 |
||
|
3 |
5 |
12 |
30 |
20 |
||
|
4 |
3 |
8 |
12 |
6 |
||
|
5 |
3 |
20 |
30 |
12 |
Обратите внимание на то, что в каждой из строк для любого многогранника будет выполняться равенство Сумма числа вершин и числа граней, без числа ребер всегда равна. Это доказал в своей теореме Леонард Эйлер и обобщил утверждение на всё множество многогранников.

С именем другого великого грека, Архимеда, связывают так называемые полуправильные многогранники (архимедовы тела). Он описал их в несохранившейся книге «О многогранниках». Имеется 13 архимедовых тел, которые получаются усечением правильных многогранников, и еще две бесконечные серии – правильные призмы и антипризмы с равными ребрами.
Вслед за Платоном предпринял попытку увязать строение Вселенной с правильными многогранниками Иоганн Кеплер, немецкий астроном и математик. Он предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.
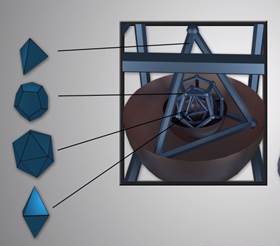
Эта модель выглядела для своего времени довольно правдоподобно. Во-первых, расстояния, вычисленные при помощи этой модели, были достаточно близки к истинным (учитывая доступную тогда точность измерения). Во-вторых, модель Кеплера давала объяснение, почему существует только шесть (именно столько было тогда известно) планет - именно шесть планет гармонировали с пятью Платоновыми телами. Однако в геометрии имя Кеплера осталось в связи с открытием им двух правильных звездчатых многогранников. Всего их четыре: другие два нашел французский математик Луи Пуансо в 1809 году.
С примерами, где можно встретиться с правильными многогранниками в архитектуре, живописи и даже в повседневной жизни, мы познакомимся на отдельном занятии, связанном с симметрией правильных многогранников. В существовании всех пяти правильных многогранников можно убедиться воочию, склеив их из разверток.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!